shivajikobardan
- 637
- 54
- Homework Statement
- difference between logistic and linear regression.
- Relevant Equations
- none
they say that linear regression is used to predict numerical/continuous values whereas logistic regression is used to predict categorical value. but i think we can predict yes/no from linear regression as well
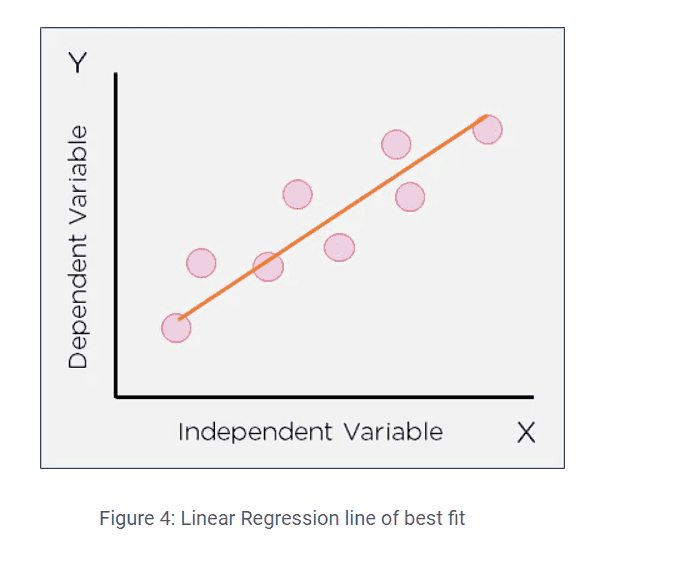
Just say that for x>some value, y=0 otherwise, y=1. What am I missing? What is its difference with this below figure?
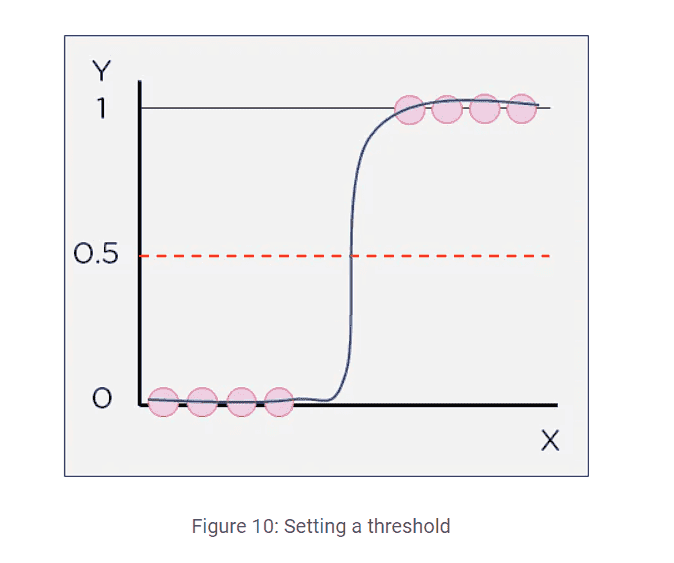
Just say that for x>some value, y=0 otherwise, y=1. What am I missing? What is its difference with this below figure?