- #1
clope023
- 992
- 132
[SOLVED] Capacitors with partial dielectrics
Consider two parallel-plate capacitors identical in shape, one aligned so that the plates are horizontal, and the other with the plates vertical
horizontal:
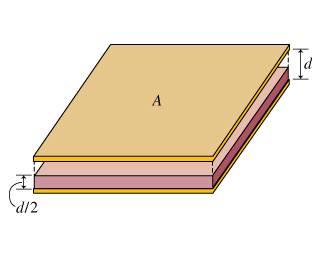
vertical:

The horizontal capacitor is filled halfway with a material that has dielectric constant . What fraction of the area of the vertical capacitor should be filled (as shown in the figure) with the same dielectric so that the two capacitors have equal capacitance? Express your answer in terms of K
e = epsilon_0
Ch (horizontal capacitance) = 2KAe/d(K+1)
Cv (vertical capacitance) = Ae(1-f+Kf)/d
I've already found the capacitance of both capacitors, however it's asking for a fraction of f by itself, I've tried a few combinations, a ratio, an equivalence and I can't seem to cancel out enough variable to get f by itself in one side such that I have an answer in terms of K, if anybody could point me in the right direction, I would greatly appreciate it.
Homework Statement
Consider two parallel-plate capacitors identical in shape, one aligned so that the plates are horizontal, and the other with the plates vertical
horizontal:
vertical:
The horizontal capacitor is filled halfway with a material that has dielectric constant . What fraction of the area of the vertical capacitor should be filled (as shown in the figure) with the same dielectric so that the two capacitors have equal capacitance? Express your answer in terms of K
Homework Equations
e = epsilon_0
Ch (horizontal capacitance) = 2KAe/d(K+1)
Cv (vertical capacitance) = Ae(1-f+Kf)/d
The Attempt at a Solution
I've already found the capacitance of both capacitors, however it's asking for a fraction of f by itself, I've tried a few combinations, a ratio, an equivalence and I can't seem to cancel out enough variable to get f by itself in one side such that I have an answer in terms of K, if anybody could point me in the right direction, I would greatly appreciate it.