- #1
John Mcrain
- 435
- 28
http://mccabism.blogspot.com/2017/08/curved-flow-and-arrows-a3.html
"The nose skirts on the Lotus 80 and Arrows A3 would have suffered from the fact that a Formula 1 car has to generate its downforce in a state of yaw. Thus, in a cornering condition, a car is subjected to a curved flow-field. This is difficult to replicate in a wind-tunnel, hence a venturi tunnel design which worked well in a straight-ahead wind-tunnel condition could have failed dramatically under curved flow conditions. To understand this better, a short digression on curved flow and yaw angles is in order.
The first point to note is that a car follows a curved trajectory through a corner, hence if we switch to a reference frame in which the car is fixed but the air is moving, then the air has to follow a curved trajectory. If we freeze the relative motion mid-corner, with the car pointing at a tangent to the curve, then the air at the front of the car will be coming from approximately the direction of the inside front-wheel, while the air at the back of the car will be coming from an outer direction.
That's the simplest way of thinking about it, but there's a further subtlety. The negotiate a corner, a car generates: (i) a lateral force towards the centre of the corner's radius of curvature; and (ii) a yaw moment about its vertical axis.
Imagine the two extremes of motion where only one of these eventualities occur. In the first case, the car would continue pointing straight ahead, but would follow a curved path around the corner, exiting at right-angles to its direction of travel. In the second case, it would spin around its vertical axis while its centre-of-mass continued to travel in a straight line.
In the first case, the lateral component of the car's velocity vector corresponds to a lateral component in the airflow over the car. The angle which the airflow vector subtends to the longitudinal axis of the car, is the same along the length of the vehicle.
In the second case, the spinning motion also induces an additional component to the airflow over the car. It's a solid body spinning about its centre of mass with a fixed angular velocity, and the tangential velocity of that spin induces an additional component to the airflow velocity along the length of the car. However, the further away a point is from the axis of rotation, the greater the tangential velocity; such points have to sweep out circles of greater circumference than points closer to the centre of mass, hence their tangential velocity is greater.
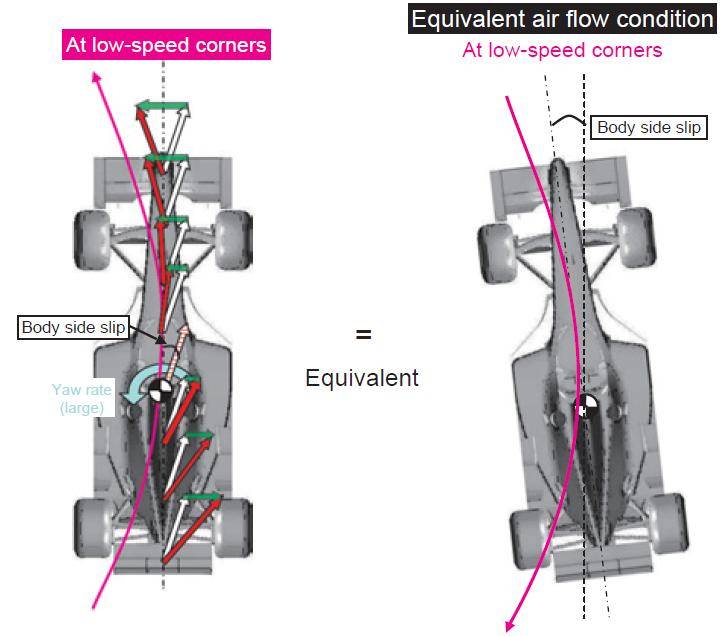
Now imagine the two types of motion combined. The result is depicted above, in the left-part of the diagram. The white arrows depict the component of the airflow due to 'side-slip': the car's instantaneous velocity vector subtends a small angle to the direction in which its longitudinal axis is pointing. In the reference frame in which the car is fixed, this corresponds to a lateral component in the direction of the airflow which is constant along on the length of the car.
When the yaw moment of the car is included (indicated by the curved blue arrow about the centre-of-mass), it induces an additional airflow component, indicated by the green arrows. Two things should be noted: (i) the green arrows at the front of the car point in the opposite direction from the green arrows at the rear; and (ii) the magnitude of the green arrows increases with distance from the centre of mass. The front of the car is rotating towards the inside of the corner, while the rear of the car is rotating away, hence the difference in the direction of the green arrows. And, as we explained above, the tangential velocity increases with distance from the axis of rotation, hence the increase in the magnitude of the green arrows.
The net result, indicated by the red arrows, is that the yaw-angle of the airflow has a different sign at the front and rear of the car, and the magnitude of the yaw angle increases with distance from the centre-of-mass. (The red arrows in the diagram are pointing in the direction in which the car is travelling; the airflow direction is obtained by reversing these arrows)."
I don't understand above explanation,can you help me.
What white arrow represent,lateral component of velocity?
*In circle exist only tangential velocity which cause tangential airflow and car is at small angle to the direction of travel,due to relative airflow coming from side.
"The nose skirts on the Lotus 80 and Arrows A3 would have suffered from the fact that a Formula 1 car has to generate its downforce in a state of yaw. Thus, in a cornering condition, a car is subjected to a curved flow-field. This is difficult to replicate in a wind-tunnel, hence a venturi tunnel design which worked well in a straight-ahead wind-tunnel condition could have failed dramatically under curved flow conditions. To understand this better, a short digression on curved flow and yaw angles is in order.
The first point to note is that a car follows a curved trajectory through a corner, hence if we switch to a reference frame in which the car is fixed but the air is moving, then the air has to follow a curved trajectory. If we freeze the relative motion mid-corner, with the car pointing at a tangent to the curve, then the air at the front of the car will be coming from approximately the direction of the inside front-wheel, while the air at the back of the car will be coming from an outer direction.
That's the simplest way of thinking about it, but there's a further subtlety. The negotiate a corner, a car generates: (i) a lateral force towards the centre of the corner's radius of curvature; and (ii) a yaw moment about its vertical axis.
Imagine the two extremes of motion where only one of these eventualities occur. In the first case, the car would continue pointing straight ahead, but would follow a curved path around the corner, exiting at right-angles to its direction of travel. In the second case, it would spin around its vertical axis while its centre-of-mass continued to travel in a straight line.
In the first case, the lateral component of the car's velocity vector corresponds to a lateral component in the airflow over the car. The angle which the airflow vector subtends to the longitudinal axis of the car, is the same along the length of the vehicle.
In the second case, the spinning motion also induces an additional component to the airflow over the car. It's a solid body spinning about its centre of mass with a fixed angular velocity, and the tangential velocity of that spin induces an additional component to the airflow velocity along the length of the car. However, the further away a point is from the axis of rotation, the greater the tangential velocity; such points have to sweep out circles of greater circumference than points closer to the centre of mass, hence their tangential velocity is greater.
Now imagine the two types of motion combined. The result is depicted above, in the left-part of the diagram. The white arrows depict the component of the airflow due to 'side-slip': the car's instantaneous velocity vector subtends a small angle to the direction in which its longitudinal axis is pointing. In the reference frame in which the car is fixed, this corresponds to a lateral component in the direction of the airflow which is constant along on the length of the car.
When the yaw moment of the car is included (indicated by the curved blue arrow about the centre-of-mass), it induces an additional airflow component, indicated by the green arrows. Two things should be noted: (i) the green arrows at the front of the car point in the opposite direction from the green arrows at the rear; and (ii) the magnitude of the green arrows increases with distance from the centre of mass. The front of the car is rotating towards the inside of the corner, while the rear of the car is rotating away, hence the difference in the direction of the green arrows. And, as we explained above, the tangential velocity increases with distance from the axis of rotation, hence the increase in the magnitude of the green arrows.
The net result, indicated by the red arrows, is that the yaw-angle of the airflow has a different sign at the front and rear of the car, and the magnitude of the yaw angle increases with distance from the centre-of-mass. (The red arrows in the diagram are pointing in the direction in which the car is travelling; the airflow direction is obtained by reversing these arrows)."
I don't understand above explanation,can you help me.
What white arrow represent,lateral component of velocity?
*In circle exist only tangential velocity which cause tangential airflow and car is at small angle to the direction of travel,due to relative airflow coming from side.
Last edited by a moderator: