Car passing a truck — calculating the relative motions

[PeroK]

Sorry for taking so long to answer, i understand now, (25m/s)t=37.5m+(18m/s)t -> 25t-18t=37.5m -> 7t=37.5m -> 5.36. Thank you @PeroK and @haruspex for bearing with me, i do appreciate it :)

Perhaps it's worth just summarising this.

There was a quick way to solve the problem, which is to take the difference in speeds of the car and the truck and the distance between them. In this case, the distance separating them was $37.5m$ and the car was traveling $7m/s$ faster than the truck. The time at which the car catches the truck is simply: $$t = \frac{37.5m}{7 m/s} = 5.36s$$
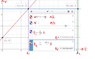
The other approach is to draw a graph of position against time of both vehicles. The point of intersection on the graph is the time at which the car catches the truck. This is related to the equations of motion as: $$x_{car} = (25m/s) t$$ and $$x_{truck} = 37.5m + (18m/s)t$$ represent straight lines on the graph and the point of intersection is the point where $$(25m/s) t = 37.5m + (18m/s)t$$ In any case, the important thing is to understand how these equations and graphs relate to the real motion and position of the vehicles.

 

[neilparker62]

Don't we need to know the length of the truck ? Since 50m behind truck means 50m behind rear of truck. Still have further displacement (if not negligible) of truck length. See other "Car passing Truck" thread below.

 

[haruspex]

50m behind truck means 50m behind rear of truck.

Not necessarily. If you are 50m behind in a race, that would be measured from front of vehicle to front of vehicle.

 

[neilparker62]

Relative velocity problem. Car traveling with initial velocity of 2m/s 50m behind "stationary" truck. Accelerates at 1.8 m/s/s till reaching 7m/s and maintains this until level with the truck. Area under graph up to t1 is 12.5m and 37.5m between t1 and t2. Simply add 18t for the actual displacement of car at t1 and t2 respectively.

Relative Velocity vs Time graph:
https://www.desmos.com/calculator/rgbooatiss

Relative Displacement vs Time graph:
https://www.desmos.com/calculator/ophyml0qrd

 

[neilparker62]

Not necessarily. If you are 50m behind in a race, that would be measured from front of vehicle to front of vehicle.

True but I think there is a problem with the ambiguity. Initially you think something is not quite right but you can't exactly place it!