- #1
FEAnalyst
- 346
- 146
Hi,
it may look like a homework but believe me that it's not. Castigliano's method was omitted when I was attending mechanics of materials course at my university and now I'm catching up. Another reason why I want to solve this is that I'm just curious what's the formula for the deflection of such beam as it can't be found in the literature.
Anyway, here's a beam that I want to solve for deflection of middle point (B) using dummy force P:
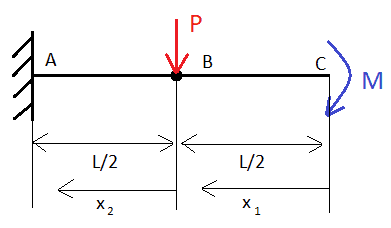
And here's my solution:
$$M(x_{1})=-M$$ $$\frac{\partial M(x_{1})}{\partial P}=0$$ $$M(x_{2})=-M-P \left( \frac{L}{2}+x_{2} \right) $$ $$\frac{\partial M(x_{2})}{\partial P}=-\frac{L}{2}-x_{2}$$ $$y_{B}=\frac{1}{EI}\int_{0}^{\frac{L}{2}} M(x) \cdot \frac{\partial M(x)}{\partial P}dx=\frac{1}{EI}\int_{0}^{\frac{L}{2}} \left( -M-P \left( \frac{L}{2}+x_{2} \right) \right) \cdot \left( - \frac{L}{2} - x_{2} \right) dx_{2} = \frac{1}{EI} \int_{0}^{\frac{L}{2}} -M \cdot \left( - \frac{L}{2}-x_{2} \right) dx_{2}=\frac{3L^{2}M}{8EI}$$
It seems fine but I solved an exemplary case and used FEA to find reference solution. This way I found out that my formula obtained from Castigliano's method is not correct. Do you have an idea what's wrong here ?
Thanks in advance for your help
it may look like a homework but believe me that it's not. Castigliano's method was omitted when I was attending mechanics of materials course at my university and now I'm catching up. Another reason why I want to solve this is that I'm just curious what's the formula for the deflection of such beam as it can't be found in the literature.
Anyway, here's a beam that I want to solve for deflection of middle point (B) using dummy force P:
And here's my solution:
$$M(x_{1})=-M$$ $$\frac{\partial M(x_{1})}{\partial P}=0$$ $$M(x_{2})=-M-P \left( \frac{L}{2}+x_{2} \right) $$ $$\frac{\partial M(x_{2})}{\partial P}=-\frac{L}{2}-x_{2}$$ $$y_{B}=\frac{1}{EI}\int_{0}^{\frac{L}{2}} M(x) \cdot \frac{\partial M(x)}{\partial P}dx=\frac{1}{EI}\int_{0}^{\frac{L}{2}} \left( -M-P \left( \frac{L}{2}+x_{2} \right) \right) \cdot \left( - \frac{L}{2} - x_{2} \right) dx_{2} = \frac{1}{EI} \int_{0}^{\frac{L}{2}} -M \cdot \left( - \frac{L}{2}-x_{2} \right) dx_{2}=\frac{3L^{2}M}{8EI}$$
It seems fine but I solved an exemplary case and used FEA to find reference solution. This way I found out that my formula obtained from Castigliano's method is not correct. Do you have an idea what's wrong here ?
Thanks in advance for your help

