Trying2Learn
- 375
- 57
- TL;DR Summary
- Prove the area projection
Hello
I am reviewing the proof of Cauchy's formula for the stress tensor and surface traction.
Without exception, every book I look at gets to the critical point of USING the projection of a triangle onto one of the three orthogonal planes.
However, I have never seen this proven.
Can someone help? Why do textbooks gloss over this? I have the projection is correct, but I have never seen a proof.
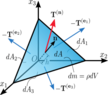
For example, in the attached figure, can someone point me to a GEOMETRIC (not algebraic with differential forms) proof that the area of the BLUE triangle, times, say, the direction cosine between its normal, and, say, the x1 axis vector, gives the area of the back wall.
I mean, long ago, Cauchy used it. So it cannot be that difficult, but I cannot prove it to myself, and every textbook I read in mechanical engineering (elasticity theory) glosses over this point. Why? I feel so stupid.
I am reviewing the proof of Cauchy's formula for the stress tensor and surface traction.
Without exception, every book I look at gets to the critical point of USING the projection of a triangle onto one of the three orthogonal planes.
However, I have never seen this proven.
- I have read hand-waving arguments about rotating the triangle and observing the result.
- I have read that it is possible to prove it easily with differential forms.
- I have read statements that one begins with the area of a triangle as half the cross product of the two vectors emanating from a common vertex.
- etc.
Can someone help? Why do textbooks gloss over this? I have the projection is correct, but I have never seen a proof.
For example, in the attached figure, can someone point me to a GEOMETRIC (not algebraic with differential forms) proof that the area of the BLUE triangle, times, say, the direction cosine between its normal, and, say, the x1 axis vector, gives the area of the back wall.
I mean, long ago, Cauchy used it. So it cannot be that difficult, but I cannot prove it to myself, and every textbook I read in mechanical engineering (elasticity theory) glosses over this point. Why? I feel so stupid.