Centripetal acceleration of viking ship in the amusement park.

[WMDhamnekar]

Hi,

Riders in an amusement park ride shaped like a Viking ship hung from a large pivot are rotated back and forth like a rigid pendulum. Sometime near the middle of the ride, the ship is momentarily motionless at the top of its circular arc. The ship then swings down under the influence of gravity.

(a) Assuming negligible friction, find the speed of the riders at the bottom of its arc, given the system’s center of mass travels in an arc having a radius of 14.0 m and the riders are near the center of mass.

(b) What is the centripetal acceleration at the bottom of the arc?

(c) Draw a free body diagram of the forces acting on a rider at the bottom of the arc.

(d) Find the force exerted by the ride on a 60.0 kg rider and compare it to her weight.

(e) Discuss whether the answer seems reasonable.

Answers:- $(a)16.57 m/s (b) 19.61 m/s^2$

(c)

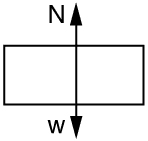N=North pole= Upward forces acting on the rider at the bottom of arc. W=?I know it is downward forces $Mass \times g(9.81 m/s^2)$

But what are your answers to (d) and (e)?

 

[skeeter]

Is there a diagram with this problem? What is the position of the ride relative to its lowest position when it is momentarily motionless?

 

[WMDhamnekar]

Is there a diagram with this problem? What is the position of the ride relative to its lowest position when it is momentarily motionless?

Hi,
I got the answer for (d) and it is 1176.798 N or $2.00 \times W$ where $W= 60 kg \times 9.80665 m/s^2$

 

[skeeter]

Hi,
I got the answer for (d) and it is 1176.798 N or $2.00 \times W$ where $W= 60 kg \times 9.80665 m/s^2$

Is that your solution, or one given by "the book"?

by the way, you didn't answer my first question ...

Is there a diagram with this problem? What is the position of the ride relative to its lowest position when it is momentarily motionless?

 

[WMDhamnekar]

Hi,
Question states 60 kg rider but give answer for 90kg rider. :)

 

[skeeter]

You still have not answered my first question ...

If the normal force on the rider is $2mg$, then the ship makes a 60 degree angle w/respect to the vertical at its highest position.

 

[WMDhamnekar]

You still have not answered my first question ...

If the normal force on the rider is $2mg$, then the ship makes a 60 degree angle w/respect to the vertical at its highest position.

Hello,
How did you compute that angle?

 

[skeeter]

Hello,
How did you compute that angle?

I used right triangle trigonometry.

 

[WMDhamnekar]

I used right triangle trigonometry.

Hello,
That means force exerted by the ride on the rider can't be more than $3mg_r$

 

[skeeter]

Hello,
That means force exerted by the ride on the rider can't be more than $3mg_r$

That's right ... as I stated in post #6, if the angle the ship makes with the vertical at its highest position is 60 degrees, then the normal force exerted on the rider is $2mg$.

You still haven't posted the original problem or any related diagram as I requested earlier in this thread. Please do so or this will be my final response.

 

[WMDhamnekar]

That's right ... as I stated in post #6, if the angle the ship makes with the vertical at its highest position is 60 degrees, then the normal force exerted on the rider is $2mg$.

You still haven't posted the original problem or any related diagram as I requested earlier in this thread. Please do so or this will be my final response.

Hello,
There is no diagram in the original question. Otherwise, I would have reproduced it here. Thanks for your response.