singh101
- 14
- 4
- Homework Statement
- I can't seem to figure out the answer for this question with formulas given.
- Relevant Equations
- Angle of rot= arc length/ radius
Angular velocity= angle of rotation/ time
v=rw (v=tangential veloctity) (w=angular velocity) r= radius
centripe acceleration= v^2/r
So my initial understanding is that it completes 5 revolutions per second. I converted the 5 rev to radians, so each revolution is 2pi. Now since I got angle of rotation I can plug it into the angular velocity formula which is Angular velocity= angle of rotation/ time. However since I don't have time I can change the formula to angle of rot x frequency. Frequency in this case would be 5. So ang Velocity is 10pi rad/s. From their on I get the tang velocity and plug it into the centrip acceleration formula, however I keep getting the wrong answer. Is there anyway to solve this with the equation given below or am I missing any equations.
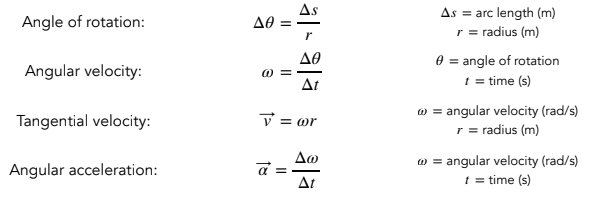

Last edited by a moderator: