Centripetal Force in a Clothesdryer

[GoldShadow]

The question is:
"In an automatic clothes dryer, a hollow cylinder moves the clothes on a vertical circle (radius r=0.32m). The appliance is designed so that the clothes tumble as they dry. This means that when a piece of clothing reaches an angle of $$\theta$$ above the horizontal, it loses contact with the wall of the cylinder and falls onto the clothes below. How many revolutions per second should the cylinder make in order that the clothes lose contact with the wall when $$\theta$$=70.0 degrees?

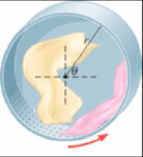I set it up like so:

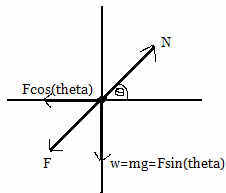
Where the center of the drawing is an article of clothing on the edge of the dryer. F is the centripetal force toward the center of the dryer, N is the normal force against the walls of the dryer. Since I'm looking for the number of revolutions per sec, I need to solve for velocity. I figure that the clothing will fall when the vertical component of the normal force is just equal to the force of gravity (mg). The vertical component of centripetal force should be equal to gravity, like I put in my diagram.

So I used mg=Fsin$$\theta$$, which I rewrote as $$mg=\frac{mv^{2}}{R}sin\theta$$. Using the given 70.0 deg for theta and 0.32m for R, and 9.8 for g, I got that v=1.83 m/s. Then I just got the circumference using 2(pi)R, which was 2.01m. Divided velocity by circumf. to get number of revolutions/sec. Final answer was 0.91 rev/sec.
Could somebody tell me if I approached this correctly at all or if I did something wrong?

 

[dynamicsolo]

I think you are mixing centripetal and centrifugal force considerations in your solution. In the reference frame of someone watching the clothes spin, N is the normal force of the drum wall on the clothing, so it should point toward the center of the drum. It is the sum of the components of the normal and weight forces along that radius of the drum that provide the centripetal force. So what would the equation for the centripetal force be?

The clothes will just break contact with the drum wall when N goes to zero. That will reduce your equation to something like what you got, but there is a critical error in what you ended up with (the units won't help you find it, because the problem is with the dimensionless trig factor). [Note: the effect on the answer turns out not to be big, because the factor that needs to be adjusted is in the neighborhood of 1, anyway...]

 

[m2003]

Your approach is correct. You correctly identified the forces acting on the clothing and used the equations for centripetal force and velocity to solve for the number of revolutions per second. Your final answer of 0.91 rev/sec is also correct. Good job!