Centroid of a semicircular arc

[bigevil]

Homework Statement

Here, I have two ways of finding the y-coordinate centroid of a semicircular arc using polar coordinates.

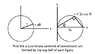
First one is considering a circle of radius a, centred at the origin. What I have done is \int ds = \int_0^{\pi} a d\theta = \pi a and then \int y ds = \int r^2 sin \theta d\theta = a^2 \int_0^{\pi} sin \theta d\theta = 2a^2, then y-centroid is 2a/π. I'm quite sure this is the right answer.

Second is a more roundabout method. It uses a circle with equation r=2a cos \theta. A right angle triangle fits inside the circle and the angle between the side passing through the origin and the x-axis is theta. But I do not get a similar answer. Here my method is to use \int y ds = \int r sin\theta \sqrt{r^2 + (\frac{dr}{d\theta})^2} d\theta = \int_0^{\frac{\pi}{2}} 2a cos \theta (2a) d\theta = 4a^2, where the limits of the integral run from 0 to half pi due to how the angle is set up. (From my working, the messy square roots part becomes just 2a.) The y-centroid for the semicircle is 4a/π, which is wrong. Can someone advise me where I have gone wrong?

The y-coordinate centroid should be the same for both as the difference between the two figures is that one is shifted a-units along the x-axis.

 

[bigevil]

Sorry, I've solved this... careless... final integral should have been 2a cos theta sin theta.