I Change of basis matrix for point group C3V

[knowwhatyoudontknow]

TL;DR Summary

Trying to understand the process for obtaining the block diagonal form of the rotation matrix for the point group C3V.

I am looking at the point group C_3v described shown here. I am trying to understand the block diagonalization process. The note says that changing the basis in the following way will result in the block diagonal form.

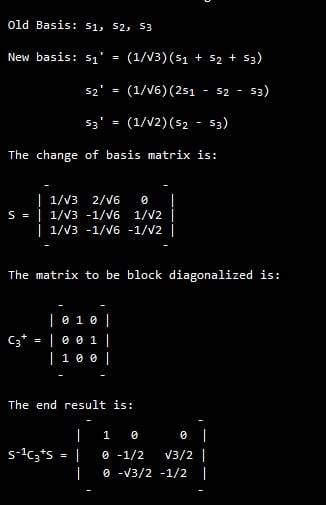
What is the rationale for choosing the new basis. Is it chosen by trial and error or is there some method behind it? I know how to generate the COB matrix using the Clebsch-Gordan coefficients in the case of angular momentum but just can't make the transition in this case. Any help would be appreciated.

 

[Mark44]

I am looking at the point group C_3v ...

What you want in BBCode is C_3v (unrendered, this looks like C_3v). In Tex, which is supported at this site, it's $C_{3v}$ (the script for this is $C_{3v}$).

.

What is the rationale for choosing the new basis. Is it chosen by trial and error or is there some method behind it?

I don't know anything about $C_{3v}$ but I do know about change of basis, one of whose most prominent applications is to diagonalize a matrix to obtain a matrix that is similar to the original matrix. Here similar has a very specific meaning. Two matrices A and B, are similar if there is an invertible matrix C such that AC = CB. Or equivalently, $B = C^{-1}AC$.
The way this is usually done is to find a new basis in terms of the eigenvectors of the original matrix, and these eigenvectors are used to form the columns of matrix C. In the event that the number of linearly independent eigenvectors is the same as the dimension of the original matrix, the matrix that is similar to the original one will be diagonal.

In your example, the resulting matrix isn't diagonal although the resulting matrix is similar to $C_3$. IOW, Final matrix = $S^{-1}C_3^+S$.

How they came up with the new basis, I have no idea, as it isn't shown in what you posted.

 

[WWGD]

Another way is using C_{3v} to Tex, using as,wraps, into $C_{3v}$. Using ##