Change of variables for multiple integrals

[kingwinner]

1) Find the volume of T bounded below by the cone z=sqrt(x²+y²) and above by the sphere x²+y²+z²=1.

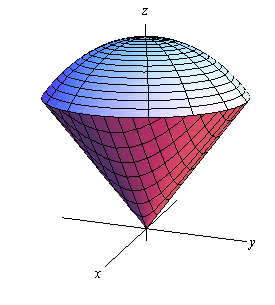
Solution:

Volume =
∫∫∫ 1 dV =
T
b d f
∫ ∫ ∫ r (d theta)dzdr (change of variables to cylindrical coordinates)
a c e
where
a=0
b=1/sqrt2 <---I am having a lot of trouble understanding this upper limit of integration for dr...clearly, not every level in the solid T have this radius (the radius is not constant in the solid T, it's part of a cone!)...help
c=r
d=sqrt(1-r²)
e=0
f=2pi

Could someone kindly explain?

 

[Defennder]

Solution:

Volume =
∫∫∫ 1 dV =
T
b d f
∫ ∫ ∫ r (d theta)dzdr (change of variables to cylindrical coordinates)
a c e
where
a=0
b=1/sqrt2 <---I am having a lot of trouble understanding this upper limit of integration for dr...clearly, not every level in the solid T have this radius (the radius is not constant in the solid T, it's part of a cone!)...help
c=r
d=sqrt(1-r²)
e=0
f=2pi

Could someone kindly explain?

Well, firstly you should note that it's not stated anywhere that having $$b=\frac{1}{\sqrt{2}}$$ implies that we are assuming that r is constant and does not vary. It just means that r is allowed to vary from 0 to 1/sqrt(2). If you're wondering how to get the upper and lower limits of the integration for r, imagine drawing a ray R from the origin, and confine R to the x-y plane. Note where it enters the projection of T onto the x-y plane and where it exits. Clearly the smallest value of R is 0, and its largest value as you can tell from the 3D image is the radius of projection of the circle where the cone and sphere meet onto x-y plane. You can check that the radius=1/sqrt(2)

 

[HallsofIvy]

The cone and the sphere meet where $z= \sqrt{x^2+ y^2}$ and $x^2+ y^2+ z^2= 1$ are both true. Squaring both sides of the first equation, $z^2= x^2+ y^2$. Then the second equation becomes $x^2+ y^2+ (x^2+ y^2)= 2x^2+ 2y^2= 2(x^2+ y^2)= 2r^2= 1$. From that, $r^2= 1/2$ or $r= 1/\sqrt{2}$. As Defennnder said, that is only for the boundary. To cover the entire volume, r must vary from 0 to $1/\sqrt{2}$.

 

[kingwinner]

Well, firstly you should note that it's not stated anywhere that having $$b=\frac{1}{\sqrt{2}}$$ implies that we are assuming that r is constant and does not vary. It just means that r is allowed to vary from 0 to 1/sqrt(2).

But I thought that to determine the integration range, we are considering how to "sweep out" dr, (d theta), and dz such that it precisely covers the whole solid. However, here if we always sweep from r=0 to r=1/sqrt2, then it cannot be part of a cone...right?

If you're wondering how to get the upper and lower limits of the integration for r, imagine drawing a ray R from the origin, and confine R to the x-y plane. Note where it enters the projection of T onto the x-y plane and where it exits. Clearly the smallest value of R is 0, and its largest value as you can tell from the 3D image is the radius of projection of the circle where the cone and sphere meet onto x-y plane. You can check that the radius=1/sqrt(2)

So for integration by change of variables to cylindrical coordinates (r,theta,z), are the integration (sweeping) range for dr and (d theta) always based on the projection of the solid onto the xy-plane? (i.e. we don't consider the z-component at all?)

 

[HallsofIvy]

But I thought that to determine the integration range, we are considering how to "sweep out" dr, (d theta), and dz such that it precisely covers the whole solid. However, here if we always sweep from r=0 to r=1/sqrt2, then it cannot be part of a cone...right?



So for integration by change of variables to cylindrical coordinates (r,theta,z), are the integration (sweeping) range for dr and (d theta) always based on the projection of the solid onto the xy-plane? (i.e. we don't consider the z-component at all?)

You are using cylindrical coordinates to do the integral. Both r and $\theta$ are in the xy-plane. You do NOT "consider the z-component" in determining them. Of course, you also integrate with respect to z.

 

[kingwinner]

2) Use "double polar coordinates" x=r(cos(theta)), y=r(sin(theta)), z=s(cos(phi)), w=s(sin(phi)) in R⁴ to compute the 4-dimensional volume of the ball x² + y² + z² + w² = R².


Um...4-dimensional ball, this is driving me crazy for a bit...but I will give it a try anyway...

My attempt:
2pi 2pi R R
∫---∫ ∫ ∫ |J|drds(d theta)(d phi)
0---0 0 0
where |J| is the Jacobian factor resulting from change of variables theorem

Is it correct? If not, can someone please teach me how to setup the integral? I am pretty confused since I can't imagine the picture of it...

 

[HallsofIvy]

Yes, what you have so far is perfectly correct, including the limits of integration. What do you get for |J|? Once you have found just integrate.

 

[kingwinner]

Yes, what you have so far is perfectly correct, including the limits of integration. What do you get for |J|? Once you have found just integrate.

But sadly, this is actually incorrect when I check my solutions manual.

In the "dr" part, the limits of integration are from 0 to some function of s, not just "R". I have absolutely no idea why...


P.S. I think |J|=rs

 

[HallsofIvy]

But sadly, this is actually incorrect when I check my solutions manual.

In the "dr" part, the limits of integration are from 0 to some function of s, not just "R". I have absolutely no idea why...

Well, yes. I didn't look closely enough before. Just look what happens if you put those parametric equations into the original equation:
[itex]x^2+ y^2+ z^2+ w^2= r^2 cos^2(\theta)+ r^2 sin^2(\theta)+ s^2 cos^2(\phi)+ s^2 sin^2(\phi)= s^2+ r^2= R^2.
The corresponding thing for circle in the plane would be $r^2= R^2$ so that r has to go from 0 (the center of the circle) to R.

Here, one of the integrals, (s if you choose it as an "outer integral") must go from 0 to R. Then, for each s, since $s^2+ r^2= R^2$ gives $r^2= R^2- s^2$. r must range from 0 to $\sqrt{R^2- s^2}$.

 

[kingwinner]

Well, yes. I didn't look closely enough before. Just look what happens if you put those parametric equations into the original equation:
[itex]x^2+ y^2+ z^2+ w^2= r^2 cos^2(\theta)+ r^2 sin^2(\theta)+ s^2 cos^2(\phi)+ s^2 sin^2(\phi)= s^2+ r^2= R^2.
The corresponding thing for circle in the plane would be $r^2= R^2$ so that r has to go from 0 (the center of the circle) to R.

Here, one of the integrals, (s if you choose it as an "outer integral") must go from 0 to R. Then, for each s, since $s^2+ r^2= R^2$ gives $r^2= R^2- s^2$. r must range from 0 to $\sqrt{R^2- s^2}$.

Thanks, but I still don't understand why it is the case that the outer integral must go from 0 to R and that the inner integral must go from 0 to sqrt(R^2 - s^2). What is the reasoning behind it?

Why can't both just go from 0 to R? The maximum radius of the ball is equal to R in every direction.

 

[HallsofIvy]

Thanks, but I still don't understand why it is the case that the outer integral must go from 0 to R and that the inner integral must go from 0 to sqrt(R^2 - s^2). What is the reasoning behind it?

Why can't both just go from 0 to R? The maximum radius of the ball is equal to R in every direction.

But not at the same time- and r and s are not independent. As I said before If put the formulas into the equation we get r²+ s²= R².
If both s and r can be as large as R then s²+ r²= 2R² not R².

If complicated situations like this are confusing, go back to simpler ones. Look at the area between the curve y= x² and the line y= 3x. x can go from 0 to 3 and y can go from 0 to 9. Would you use those as the limits of integration (no, because x= 0 to 2 and y= 0 to 9 would be a rectangle.

 

[kingwinner]

But not at the same time- and r and s are not independent. As I said before If put the formulas into the equation we get r²+ s²= R².
If both s and r can be as large as R then s²+ r²= 2R² not R².

If complicated situations like this are confusing, go back to simpler ones. Look at the area between the curve y= x² and the line y= 3x. x can go from 0 to 3 and y can go from 0 to 9. Would you use those as the limits of integration (no, because x= 0 to 2 and y= 0 to 9 would be a rectangle.

How about theta and phi? Why can they BOTH go from 0 to 2pi?

This is very confusing

 

[kingwinner]

How about theta and phi? Why can they BOTH go from 0 to 2pi?

This is very confusing

Any further explanation on this?

 

[HallsofIvy]

How about theta and phi? Why can they BOTH go from 0 to 2pi?

This is very confusing

Any further explanation on this?

I'm wondering why you would think anything else! Sine and cosine have period 2$\pi$ so that would be kind of expected.

 

[kingwinner]

OK!

Now, I have another related question:

Generally, how can we find the projection of a solid onto the coordinates?

I. Consider the solid V in R^3 bounded by the parabolic cylinder x=y^2, and the planes z=0, and x+z=1. How can I find the projection of V onto the yz-plane, for example?

II. Consider the solid S in R^3 bounded by y=sqrt(x), x=0, z=0, and z=4-y^2. How can I find the projection of V onto the xz-plane, for example?

I can visualize both solids above, but I can't visulaize or solve for the projection...

Thanks again!

 

[HallsofIvy]

I. On the yz-plane, x= 0, of course. The projection of the point (x,y,z) onto the yz-plane is (0, y, z). In particular, every point satisfying y= x², (x, x², z) projects to (0, 0, z). Every point of (x, y, 0) projects to (0, y, 0), and every point satisfying x+z= 1, (x, y, 1-x), projects to (0, y, 1). The projection of V onto the yz-plane has the lines y= 0, z= 0, and z= 1 as boundary. It is the infinitely long strip between z= 0 and z= 1, and above y= 0.

II. Every point in the xz-plane has y= 0. The projection of the point (x, y, z) onto the xz-plane is (x, 0, z). $y= \sqrt{x}$ projects to $0= \sqrt{x}$ or x= 0. x= 0 and z= 0, since they do not involve y, project to themselves. Finally, z= 4- y² projects to the line z= 4. The projection of S again projects to an infinite strip, this time bounded by the lines x= 0, z= 0, and z= 4.

 

[Krypton]

How can i find the new limits of integration when change of variables are done to a double integral ,without graphing the function. ? Some one please reply

 

[Defennder]

You can use inequalities for both variables to determine the new limits.