tellmesomething
- 449
- 68
- Homework Statement
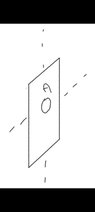
- Three identical metal plates with large surface areas are kept parallel to each other as shown in the figure. The leftmost plate is given a charge Q, the rightmost a charge -2Q and the middle one remains neutral. Find the charge appearing on the outer surface of the rightmost plate
- Relevant Equations
- None
View attachment 348052
I took a point P on the conductor with charge Q. We know that the field inside a conductor is zero in electrostatic equilibrium
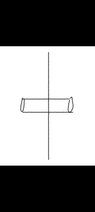
Therefore I took induced charge on the neutral conductor to be x and gave the respective charges to the others. On the side facing conductor with charge Q the neutral one has an induced charge of -x and the induced charge on the inner side Of conductor with charge Q is x so the outer part has Q -x.
Similarly the other side of the neutral sheet has x charge and the inner side of the rightmost sheet has -x charge while the outer side has -2Q + x charge
Field at point P due to all the charges =0

The arrows are the direction of fields
As we can see the direction for field produced by Q-x and -2Q+x would be the same.
But my x ends up cancelling.
I dont know what is going wrong here pls help?
I took a point P on the conductor with charge Q. We know that the field inside a conductor is zero in electrostatic equilibrium
Therefore I took induced charge on the neutral conductor to be x and gave the respective charges to the others. On the side facing conductor with charge Q the neutral one has an induced charge of -x and the induced charge on the inner side Of conductor with charge Q is x so the outer part has Q -x.
Similarly the other side of the neutral sheet has x charge and the inner side of the rightmost sheet has -x charge while the outer side has -2Q + x charge
Field at point P due to all the charges =0
The arrows are the direction of fields
As we can see the direction for field produced by Q-x and -2Q+x would be the same.
But my x ends up cancelling.
I dont know what is going wrong here pls help?