- #36
Saitama
- 4,243
- 93
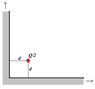
tiny-tim said:no, i meant taking advantage of one of the basic symmetries of the whole set-up
(and remember, when you have a conductor, part of your gaussian surface is likely to be along the middle of it)
you might get a clue by working backwards from the answer … what do you need the charges to be?
But if I select a gaussian surface in the middle, far from both the ends, it won't include the charge Q/2. I am honestly lost.
Chestermiller said:It's also possible to "brute force" the solution if you know the equation for the surface charge distribution induced on an infinite flat sheet by a point charge q located at a distance h from the sheet. This would involve doing some integration. This method gives the Q/4 given results you alluded to earlier (PA), but, with the opposite signs.
I am very sorry for the confusion, the given answers are indeed opposite. Sorry again.

But how do you approach it through integration?