Circle of Cylinders: Finding Length & Area

[Evales]

I have an EPW that I don't quite know how to get started.
Below is the EPW question and then after that is what I am stuck with.


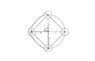
There are n identical cylinders glued upright to a board. Each cylinder has a radius of r and that centers of their bases lie on a large cirlce of radius R They are even spaced around the circle. A loop of wire encloses the cylinders.

Find in terms of n, r and R,
1. The length of the loop
2. The area contained by the loop
3. Do these formulae hold when there are two cylinders?

I was wondering how you find the amount of the wire that is around the cylinder. Surely it changes for the number of cylinders, but how? Also for question 2 I will need a way to calculate the angle. My working is below:
Using two cylinders as an example, the circumference of an entire circle in looped with wire is eventually made as it loops around both of the cylinders and connects together, so perhaps the amount of wire touching each cylinder = (circumference of the cylinder)/n but judging from the existence of question 3 I could be wrong, can someone confirm my answer?

By the way, I understand picturing these questions may be hard, try drawing a quick diagram of the two cylinder thing and perhaps 3 cylinders (it helps)

Also, Math Help Forum is not working, does anyone know why?

 

[Defennder]

Just to clarify something, the cylinders are positioned such that they are tightly packed within the circle on the board? And does this imply that the cylindrical bases do not cross the circumference of the circle on the board with radius R?

 

[Evales]

No the center of the cylinders lie on the circumference of the large circle R.

Look at my diagram it makes it easier.

I have now found that the length of the wire can be given by:

(2Rn) sin(pi/n) + r(phi)

Bare in mind (in relation to my diagram) That:
Theta = (2pi/ n)
The length of a chord = (2r) sin[(1/2)(theta)]

I simply don't know what phi is. I think that phi is equal to theta. But I don't have any mathematical proof.

And anyone help me with the mathematical proof?

 

[Evales]

And anyone help me with the mathematical proof?

**Can anyone help me with the mathematical proof?

 

[HallsofIvy]

It seems to me to be a simple problem. The large circle has radius R. On it you center a smaller circle of radius r. One point of that smaller circle, then, will haved distance r+ R from the center of the larger circle. It looks to me like the loop of wire will be an n-gon with circum-radius R+r.

 

[Evales]

HallsofIvy

I don't quite understand what you mean are you saying there is only one circle?