- #1
Steve13579
- 12
- 0
I am hoping that general physics is the correct location for this problem, but if I am wrong please say so. I have a problem where two capacitors of different value are in series and are attached to a DC source.
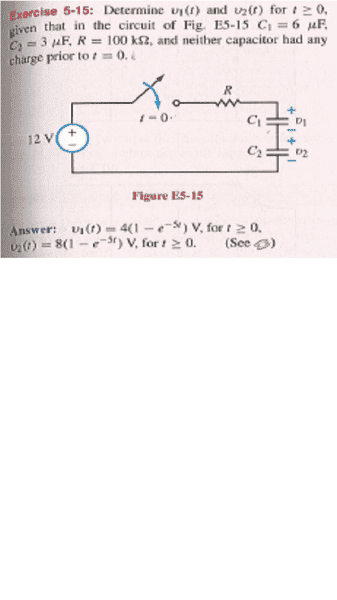
Image is a bit blurry but that is how our professor scanned it. This is practice he said we should do, and I solved it for V total but not individually.
relevant formulas: C(dv/dt) tou=RC
attempt at solution:
at t=0; v=0
at t=∞; v=12
(v-12)/100k + c(dv/dt) = 0
(dv/dt) + 5v = 60
than solving the differential equation I get
v = c1e-5t + 12
solving for c1 I got the final solution
v(t) = -12e-5t + 12
How would I go about solving individually? And did I even get the correct solution? It is logical for t=0 being 0v and at t=∞ getting 12v
Thanks,
Steve
Homework Statement
Image is a bit blurry but that is how our professor scanned it. This is practice he said we should do, and I solved it for V total but not individually.
relevant formulas: C(dv/dt) tou=RC
attempt at solution:
at t=0; v=0
at t=∞; v=12
(v-12)/100k + c(dv/dt) = 0
(dv/dt) + 5v = 60
than solving the differential equation I get
v = c1e-5t + 12
solving for c1 I got the final solution
v(t) = -12e-5t + 12
How would I go about solving individually? And did I even get the correct solution? It is logical for t=0 being 0v and at t=∞ getting 12v
Thanks,
Steve
Last edited: