- #1
Jimmy87
- 686
- 17
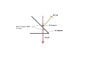
Homework Statement
I have attached questions about gravitron. I'm struggling with question 2 about calculating the normal force of the gravitron.
Homework Equations
mv^2/r
The Attempt at a Solution
I know the answer so I can figure it out as I know it involves setting the Ncos(62) = mg (N = normal force) but I don't get how you know the angle involved is 62 as it only gives you the angle the track makes with the floor?
Also, please could someone explain why the track is tilted as appose to being vertically upright and what this has to do with enabling the track to slide up when its rotating?