Clarification on Rindler coordinates definition

[cianfa72]

TL;DR Summary

Clarification about the definition of Rindler coordinates with respect to the observers's proper acceleration profile.

Hi,

starting from this post Basic introduction to gravitation as curved spacetime I would ask for a clarification about Rindler coordinates.

From this wiki entry Rindler coordinates I understand that the following transformation (to take it simple drop $y,z$)

$$T = x\sinh{(\alpha t)} , X=x\cosh{(\alpha t)}$$
with $\alpha$ parameter fixed leads to the worldlines of a family of accelerating observers (bodies) each with the given proper acceleration $\alpha$. For example the following picture (from the above link) represents the case $\alpha=0.5$. Each observer in this family (congruence) is identified by a different value of the $x$ coordinate.

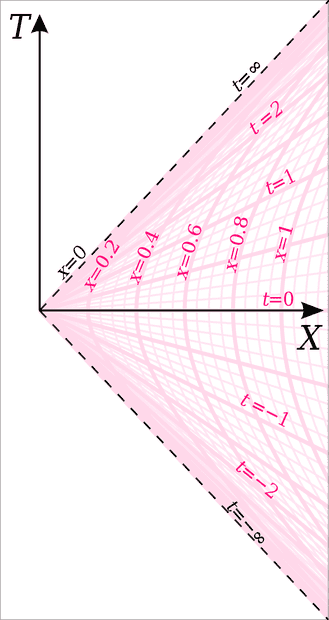
Now, if I understand correctly, the proper time of each observer (i.e. the proper time read by its wristwatch) is set to $0$ when their worldlines intersect the X axis of the Lorentzian coordinate chart. Thus if we consider for example the curve $t=1$ it intersects the observers hyperbolas in a point (an event) in which the proper time $\tau$ read by each observer's wristwatch is actually $\tau=1$.

If the above a correct, I'm not sure if it actually makes sense to call that family of observers as "Rindler observers" since they have the same profile of proper acceleration (e.g. $\alpha=0.5$ as in the above picture).

Thank you.

 

[DrGreg]

First note we are using coordinates in which $c = 1$.

The proper acceleration of a particle at a fixed value of $x$ is $1 / x$. (In particular, $\alpha$ when $x = 1 / \alpha$.)

The proper time $\tau$ and the Rindler coordinate time $t$ for a particle at a fixed value of $x$ are related by $\text{d} \tau = \alpha x \, \text{d} t$. (In particular, $\text{d} \tau = \text{d} t$ when $x = 1 / \alpha$.) This follows from the metric$$
\text{d} s^2=-\alpha^2 x^2 \, \text{d} t^2 + \text{d} x^2.
$$

 

[cianfa72]

The proper acceleration of a particle at a fixed value of $x$ is $1 / x$. (In particular, $\alpha$ when $x = 1 / \alpha$.)

So, just to fix ideas, set the parameter $\alpha=0.5$ as in the wiki page. The worldline of Rindler observer described by $x=1/0.5=2$ is the worldline of the observer accelerating with proper acceleration $0.5$ (it is not shown in the above picture from wiki page).

For this Rindler observer (and for this only) we have $\tau=t$. Then if we take for example the curve $t=1$ depicted in the inertial chart it intersects the worldline of the $x=2$ observer at the event for which its proper time $\tau=t=1$. For all other Rindler observers their 'elapsed' proper time $\tau$ is related to the coordinate time $t=1$ (at the intersection point) through their $x$ coordinate value (i.e. their proper acceleration $1/x$).

So basically the Rindler coordinate time $t$ in the Rindler chart is exactly the same as the proper time $\tau$ of the $x=2$ Rindler observer (not others).

Is that correct ? Thanks.

 

[DrGreg]

Is that correct ?

Yes.

 

[cianfa72]

ok, so basically the role of parameter $\alpha$ is just to select which Rindler observer is actually employed to define the coordinate time $t$ for the Rindler chart -- for example, choosing $\alpha=1$ does mean the proper time $\tau$ of Rindler observer described by $x=1$ is actually employed to define the coordinate time $t=\tau$ for the Rindler chart.

Coming back to the thread mentioned in the OP, I believe the simultaneity definition implied by the Rindler chart is as follows (as above drop $y,z$ dimensions):

Take a family (a congruence) of Rindler observers each with a wristwatch: set their wristwatch reading to $0$ when their worldlines intersect the X axis of the global inertial frame. Then employ the wristwatch reading (proper time $\tau$) of one specific observer in the family to define the coordinate time $t$ for the Rindler chart being defined.

Does it make sense ? Thanks.

 

[DrGreg]

Take a family (a congruence) of Rindler observers each with a wristwatch: set their wristwatch reading to $0$ when their worldlines intersect the X axis of the global inertial frame. Then employ the wristwatch reading (proper time $\tau$) of one specific observer in the family to define the coordinate time $t$ for the Rindler chart being defined.

This is correct as far as it goes but it's incomplete: it doesn't explicitly say how you extend the proper time of the "specific observer" to become the coordinate time of all observers. Or in other words it doesn't specify what the lines of constant $t$ look like, i.e. that they should, in a $(T, X)$ coordinate diagram, look like straight lines through the origin.

Mathematically you can specify that the planes of simultaneity must be orthogonal to the congruence of observer worldlines.

Or, less abstractly, you can say that what is simultaneous to an event on the "specific observer's" worldline is determined by a momentarily comoving inertial observer i.e. using the standard Einstein synchronisation method for inertial observers.

Other simultaneity conventions are possible. The Wikipedia article discusses "radar coordinates" a.k.a. "Lass coordinates" which are not the same as the Rindler coordinates being discussed here. (They use the same method as Einstein synchronisation but with a non-inertial observer.) In the limit as the distance between two observers tends to zero, Rindler simultaneity and Lass simultaneity become the same.

 

[cianfa72]

This is correct as far as it goes but it's incomplete: it doesn't explicitly say how you extend the proper time of the "specific observer" to become the coordinate time of all observers. Or in other words it doesn't specify what the lines of constant $t$ look like, i.e. that they should, in a $(T, X)$ coordinate diagram, look like straight lines through the origin.

Mathematically you can specify that the planes of simultaneity must be orthogonal to the congruence of observer worldlines.

Or, less abstractly, you can say that what is simultaneous to an event on the "specific observer's" worldline is determined by a momentarily comoving inertial observer i.e. using the standard Einstein synchronisation method for inertial observers.

ok, but it could be done as follows:

For each of Rindler "non specific" observers 'adjust' the 'natural' rate of their wristwatches scaling them by a factor $1/x$ depending on the coordinate value $x$ that 'labels' each of them.

Thus for instance fixing $\alpha=1$ the proper time of the $x=1$ observer (the specific one) becomes the chart coordinate time $t$. For all other observers just scale their proper time by $1/x$ to get the chart coordinate time $t$.

 

[DrGreg]

ok, but it could be done as follows:

For each of Rindler "non specific" observers 'adjust' the 'natural' rate of their wristwatches scaling them by a factor $1/x$ depending on the coordinate value $x$ that 'labels' each of them.

Thus for instance fixing $\alpha=1$ the proper time of the $x=1$ observer (the specific one) becomes the chart coordinate time $t$. For all other observers just scale their proper time by $1/x$ to get the chart coordinate time $t$.

Yes, that works and gives the same result.

 

[cianfa72]

Mathematically you can specify that the planes of simultaneity must be orthogonal to the congruence of observer worldlines.

ok, so that does mean consider the (timelike) tangent vector (4-velocity) at each point along the observer's worldlines in the congruence and take the orthogonal complement to it w.r.t. the Lorentz metric in flat spacetime.

 

[DrGreg]

ok, so that does mean consider the (timelike) tangent vector (4-velocity) at each point along the observer's worldlines in the congruence and take the orthogonal complement to it w.r.t. the Lorentz metric in flat spacetime.

Yes.

 

[cianfa72]

Therefore the value of parameter $\alpha$ affects only how lines of constant $t$ looks like in global inertial $(T,X)$ coordinate chart (lines of constant $x$ are not affected). Two Rindler chart differ only in the family of straight lines of constant $t$ through the origin.

Thanks for your time.

 

[pervect]

Rindler coordinates are much more intuitive in a noncoordinate basis, aka a nonholonomic I'm not sure how familiar you are with such a basis. Let's start with a review of coordinate bases, which will hopefully be familiar. If it's not, it's rather an important stepping stone to understand coordinate bases first.

In a coordinate basis (t,x,y,z) the basis vectors at any point in the manifold are mathematically defined by differential operators, ($\partial / \partial t, \partial / \partial x, \partial / \partial y, \partial / \partial z).$ These can be and often are written instead as $\partial_t, \partial_x, \partial_y, \partial_z$.

Caroll, amongst other authors, goes over this in their lecture notes. There is a lot of background, but the part I will be focusing on is this, from page 44 of https://preposterousuniverse.com/wp-content/uploads/grnotes-two.pdf

Thus the partials {$\partial_\mu$} do indeed represent a good basis for the vector space of directional
derivatives which we can therefore safely identify with the tangent space.

I suppose you don't necessarily need to know everything Caroll writes, but you do need to know that tensors are expressed in terms of basis vectors, and that basis vectors are mathematically tied to derivative operators.

As a reminder, every point in a manifold has its own unique tangent space. Vectors must be able to add and scale commutatively. In a manifold, displacements are not vectors because they do not satisfy this condition, but in the tangent space of a manifold, vectors DO satisfy this. And locally, we can map the tangent space to the manifold itself via what's called the "exponential map", which I won't get into.

The advantage of a coordinate basis is that the Christoffel symbols of the basis are defined from and computed by the partial derivatives of the metric tensor. Wiki mentions this, a bit opaquely.

https://en.wikipedia.org/wiki/Christoffel_symbols#Definition_in_Euclidean_space

Using that the symbols are symmetric in the lower two indices, one can solve explicitly for the Christoffel symbols as a function of the metric tensor by permuting the indices and resumming:[11]

$${\displaystyle {\Gamma ^{i}}_{kl}={\frac {1}{2}}g^{im}\left({\frac {\partial g_{mk}}{\partial x^{l}}}+{\frac {\partial g_{ml}}{\partial x^{k}}}-{\frac {\partial g_{kl}}{\partial x^{m}}}\right)}$$

The Christoffel symbols are most typically defined in a coordinate basis, which is the convention followed here. In other words, the name Christoffel symbols is reserved only for coordinate (i.e., holonomic) frames. However, the connection coefficients can also be defined in an arbitrary (i.e., nonholonomic) basis of tangent vectors

Note that as wiki states, these important formula are ONLY valid in a coordinate basis, not a noncoordinatge basis.

A noholonomic basis is in fact, what we're about to utilize. I should note that GRTensor, for one, makes directly using such a basis much easier, but I'm afraid I don't know what other programs might help. In general, though, the mathematical manipulations are involved enough that compuatational assistance of some sort is EXTREMELEY helpful. There are some other threads on available tools, the free ones I'm aware of are sagemath (with the tensor package) and Maxima.

The "problem" with the coordinate basis is that the vectors are not unit length, as can easily be seen from looking at the metric tensor $g_{ij}$. In particular, the length of the basis vector $\partial_t = \partial / \partial t$, which is just the length of the vector with components (1,0,0,0) in the coordinate basis is $g_{00}$, which is not unity. Note that we are assigning 0 to the index of time here, a common convention.

The sort of nonholonomic basis we are interested in is the orthonormal basis. Physical interpretation of the significance of the components of the vectors is much clearer in an orthonormal basis, as that's the sort of basis we routinely use.

In the coordinate basis, as other posters have mentioned, the proper accleration vector $a_b = u^a \nabla_a u^b$ has components of (0, 1/x). In the orthonormal basis, it has components (0,1), emphasizing the fact that the accleration vector is of unit length everywhere.

Unless you want to get into Ricci rotation coeffecients (which I do not - the program I generally run uses them, but I do not), you're stuck, as far as I know, with using the coordinate basis for calculational purposes to compute the covariant derivatives, such as $\nabla_a$ in the expression $a^b = u^a \nabla_a u^b$ for the acceleration vector. Then you can converting back from the coordinate basis into the orthonormal basis. GRTensor (and perhaps other programs) allow one to work directly in the orthonormal basis. The physical interpretation is greatly aided , in my opinion, by the use of an orthonormal basis, in fact, that's one of the many possible definitions of a "frame of reference", a set of basis vectors. And when the set of basis vectors all have unit length and are orthogonal, they are much easier to interpret physically.

Perhaps when I have some time I'll draw the coordinate basis vectors for polar coordinates (r, theta) as an example to show the difference between a coordinate and an orthonormal basis, but at the moment I have to run.

 

[PeterDonis]

In the coordinate basis, as other posters have mentioned, the proper accleration vector $a_b = u^a \nabla_a u^b$ has components of (0, 1/x).

Yes; and since $g_{xx} = 1$ in this basis, the length of this vector is also $1 / x$.

In the orthonormal basis, it has components (0,1), emphasizing the fact that the accleration vector is of unit length everywhere.

As the above makes clear, this is not correct. The components of a vector purely in the $x$ direction are the same in the orthonormal basis as in the coordinate basis, since $g_{xx} = 1$ in the coordinate basis.

Physically, it should be obvious that the length of the proper acceleration vector must vary with $x$, since that length is the actual acceleration that an observer will feel, and that varies with $x$.

 

[pervect]

My bad, the acceleration vector (0,1/x) is the proper acceleration of an observer with constant rindler coordinate x, which indeed approaches infinity as x approaches zero and has a magnitude of 1/x. The acceleration vector in the orthonormal basis is also (0, 1/x). That's what I get for posting in a rush without actually calculationg everything to verify.

 

[cianfa72]

the acceleration vector (0,1/x) is the proper acceleration of an observer with constant rindler coordinate x, which indeed approaches infinity as x approaches zero and has a magnitude of 1/x. The acceleration vector in the orthonormal basis is also (0, 1/x).

ok, as far as I can understand we can actually calculate the Christoffel symbols in the holonomic (coordinate) basis associated to the Rindler chart starting from the expression of metric tensor $g_{\mu \nu}$ in that chart. Then we get an expression for the covariant derivative operator $\nabla_a$ in that (Rindler) chart. We can use it to calculate the acceleration 4-vector of Rindler's observers along their worldlines. It has $(0,1/x)$ components in that coordinate basis.

So far so good. Then we move to an orthonormal non-holonomic basis derived from it. Since the holonomic basis associated to the Rindler chart is orthogonal, we can simply "normalize" the length of the coordinate timelike vector. Hence for a vector purely in $x$ direction such as the Rindler's observers acceleration, its components do not change -- i.e. they are $(0,1/x)$ as well.

I hope the above is correct. Thank you.

 

[PeterDonis]

ok, as far as I can understand we can actually calculate the Christoffel symbols in the holonomic (coordinate) basis associated to the Rindler chart starting from the expression of metric tensor $g_{\mu \nu}$ in that chart. Then we get an expression for the covariant derivative operator $\nabla_a$ in that (Rindler) chart. We can use it to calculate the acceleration 4-vector of Rindler's observers along their worldlines. It has $(0,1/x)$ components in that coordinate basis.

So far so good.

Yes., all correct.

Then we move to an orthonormal non-holonomic basis derived from it. Since the holonomic basis associated to the Rindler chart is orthogonal, we can simply "normalize" the length of the coordinate timelike vector. Hence for a vector purely in $x$ direction such as the Rindler's observers acceleration, its components do not change -- i.e. they are $(0,1/x)$ as well.

Yes. The only comment I would add is that the spatial basis vector in the holonomic basis is already a unit vector, so it doesn't need to be normalized; that's why the only basis vector that changes when we go to the orthonormal basis is the timelike one.

 

[pervect]

ok, as far as I can understand we can actually calculate the Christoffel symbols in the holonomic (coordinate) basis associated to the Rindler chart starting from the expression of metric tensor $g_{\mu \nu}$ in that chart. Then we get an expression for the covariant derivative operator $\nabla_a$ in that (Rindler) chart. We can use it to calculate the acceleration 4-vector of Rindler's observers along their worldlines. It has $(0,1/x)$ components in that coordinate basis.

So far so good. Then we move to an orthonormal non-holonomic basis derived from it. Since the holonomic basis associated to the Rindler chart is orthogonal, we can simply "normalize" the length of the coordinate timelike vector. Hence for a vector purely in $x$ direction such as the Rindler's observers acceleration, its components do not change -- i.e. they are $(0,1/x)$ as well.

I hope the above is correct. Thank you.

Yes, that looks good. The only thing I'd add is that if you want to covert to SI units, you want to convert inverse meters into meters / second^2. This is done by multiplying by c^2. Thus, in SI units, or in any non-geometric units, the acceleration is c^2 / x. In geometric units c^2=1 and we get the original expression.