Classic Incline problem with cylinder

[member 731016]

Homework Statement

Please seee below

Relevant Equations

Please seee below

FOr this,

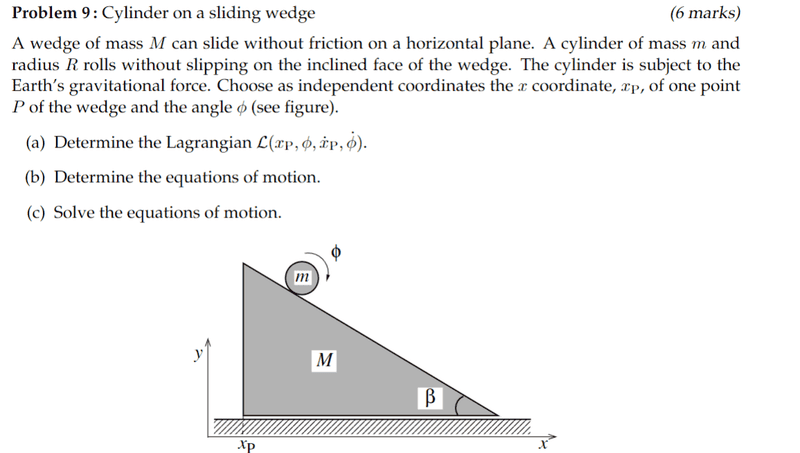
Use alternate coordinate system

With $ȳ$-axis parallel to incline and $x̄$-axis parallel to the x-axis. Kinetic energy using this alternate coordinate system is $T = \frac{1}{2}M\dot x_p^2 + \frac{1}{2}mR^2\dot \phi^2 + \frac{1}{2}m(\dot x̄^2 + \dot ȳ^2 + 2\dot x̄ \dot ȳ \cos\beta)$ and potential energy is $V = -mgȳ\sin \beta$. Note how potential energy of block was not included as we don’t know where the height of the COM is, however, it is a constant, so we can just all the high c, and it will add a $+C$ to the lagrangian

Now transform to original x-y coordinate system using transformations $ȳ = -\frac{y}{sin \beta}$ and $x̄ = x + y\cot \beta$ from decomposing $ȳ$ along the x and y axes. I think that $\hat ȳ = \hat i - \hat j$. Then one would substitute the these transformations into the kinetic energy and potential energy expressions, however, how does one the $x$ and $y$ in these transformations in terms of $x_p$ and $\phi$.

Thanks!

 

[anuttarasammyak]

The cylinfer has velocity of
x direction : $R\dot{\phi} \cos \beta + \dot{x}_P$
y direction : -$R\dot{\phi} \sin \beta$
and potential energy of $-mgR\phi \sin \beta$ which is 0 for $\phi$= 0

 

[haruspex]

$\frac{1}{2}m(\dot {\bar x}^2 + \dot {\bar y}^2 + 2\dot {\bar x} \dot {\bar y} \cos\beta)$

Check: does that give the right answer when $\beta=0$?
Btw, the latex works better using \dot{\bar x}.

I think that $\hat ȳ = \hat i - \hat j$.

Very unlikely that $\hat i - \hat j$ would happen to have unit magnitude, but I'm not sure how you are defining them.

 

[member 731016]

The cylinfer has velocity of
x direction : $R\dot{\phi} \cos \beta + \dot{x}_P$
y direction : -$R\dot{\phi} \sin \beta$
and potential energy of $-mgR\phi \sin \beta$ which is 0 for $\phi$= 0

Check: does that give the right answer when $\beta=0$?
Btw, the latex works better using \dot{\bar x}.

Very unlikely that $\hat i - \hat j$ would happen to have unit magnitude, but I'm not sure how you are defining them.

@anuttarasammyak @haruspex

Thank you both for your replies!

I see how you got the relation for y by using the rolling condition vector decomposition. However, sorry I am confused how you got the relation for x. I get everything apart from the + time derivative of x_p term. Do you please know why it is the time derivative of x_p not the time derivative of x (since it is along the x-axis)?

Also yes, I think that the expression I found the the cylinder velocity works for the special case of $\beta = 0$. However, it is strange to think about since I already defined a non-orthogonal coordinate system to be parallel to the incline for the current $\beta$ shown in the diagram, so I assume the coordinate system would remain fixed if we change the beta. However, there is a potential option that we could redefine the coordinate system again. Do you please know whether you intended for the coordinate system to also be rotated too as $\beta$ approaches zero or is it just meant to be fixed?

Thanks!

 

[kuruman]

Also yes, I think that the expression I found the the cylinder velocity works for the special case of β=0. However, it is strange to think about since I already defined a non-orthogonal coordinate system to be parallel to the incline for the current β shown in the diagram, so I assume the coordinate system would remain fixed if we change the beta. However, there is a potential option that we could redefine the coordinate system again. Do you please know whether you intended for the coordinate system to also be rotated too as β approaches zero or is it just meant to be fixed?

Setting $\beta =0$ is just a way to verify that you have the correct form for the kinetic energy. If it is correct, it should work for any $\beta.$ Of course, the task in this case becomes a bit of a challenge to the unwary reader.. Of all the choices of symbols at your disposal you had to pick $y$ for the direction down the incline and ignore that $x$ and $y$ are already defined in the drawing as the standard Cartesian coordinates. So when $\beta =0$, your $y$ becomes the already defined $x$ and is orthogonal to the already defined $y$. That's confusing.

If I were doing this, I would pick $s$ as the generalized coordinate along the incline, with $s=0$, say, at the upper corner of the wedge and proceed from there. Note that when $\beta =0$, $s\rightarrow x$.

 

[haruspex]

You still have not said how you define $\hat i, \hat j$. If those are $\hat x, \hat y$ then I get $\hat{\bar y}=\cos(\beta)\hat i-\sin(\beta)\hat j$.

 

[anuttarasammyak]

Do you please know why it is the time derivative of x_p not the time derivative of x (since it is along the x-axis)?

x_p is x coordinate of the rectangle corner (or any other part fixed point is OK) of the moving triangle. What is x you mentioned ?

 

[haruspex]

The cylinfer has velocity of
x direction : $R\dot{\phi} \cos \beta + \dot{x}_P$

@ChiralSuperfields is using $x$ as the same as $x_P$ and $\bar x = x_P+R{\phi} \cos \beta$.

 

[member 731016]

Setting $\beta =0$ is just a way to verify that you have the correct form for the kinetic energy. If it is correct, it should work for any $\beta.$ Of course, the task in this case becomes a bit of a challenge to the unwary reader.. Of all the choices of symbols at your disposal you had to pick $y$ for the direction down the incline and ignore that $x$ and $y$ are already defined in the drawing as the standard Cartesian coordinates. So when $\beta =0$, your $y$ becomes the already defined $x$ and is orthogonal to the already defined $y$. That's confusing.

If I were doing this, I would pick $s$ as the generalized coordinate along the incline, with $s=0$, say, at the upper corner of the wedge and proceed from there. Note that when $\beta =0$, $s\rightarrow x$.

You still have not said how you define $\hat i, \hat j$. If those are $\hat x, \hat y$ then I get $\hat{\bar y}=\cos(\beta)\hat i-\sin(\beta)\hat j$.

x_p is x coordinate of the rectangle corner (or any other part fixed point is OK) of the moving triangle. What is x you mentioned ?

@ChiralSuperfields is using $x$ as the same as $x_P$ and $\bar x = x_P+R{\phi} \cos \beta$.

Thank you for your replies @kuruman, @haruspex and @anuttarasammyak!

Re: Coordinate system. I agree, sorry about that.

Re: Unit vector. Yes, sorry, that is my mistake, that makes sense the unit vector is that.

Re: x vs x_p coordinate. I don't think that x is the same as x_p since x_p ∈ x in the x-y coordinate system (Not x-bar, y-bar coordinate system). The x bar is in the different coordinate system with the x bar and y bar axes. The x that I for the x and y axes.

Thanks!

 

[member 731016]

Also does someone please know what the GPE of the block is? Is it ok if I just say the heigh of the COM is y = -k, where k is a constant?

For (c), I am trying to solve the equations of motion. In terms of integration constants, I solve the second order ODE coupled system and I have $\phi = ht + k$ and $x_p = wt + c$. However, does someone please know what is good assumption to make to find Inital conditions?

I was thinking $\phi(0) = \phi_{qi}$, $\dot \phi(0) =\dot \phi_{qi}$ $x_p(0) = x_{2e}$ $\dot x_p(0) = \dot x_{2e}$

Thanks!

 

[anuttarasammyak]

The x that I for the x and y axes.

Does your "x" or "time derivative of x" have something to do with the Lagrangian of

? I do not find it in parameter of the Lagrangian.

 

[member 731016]

Does your "x" have something to do with the Lagrangian of
View attachment 344176
? I do not find it in parameter of the Lagrangian.

Thank you for your reply @anuttarasammyak!

Sorry I am confused what you are saying. Do you please mean that I need $\phi$ and $x_p$ axes?

That is a interesting idea to consider. However, do you please know how one would draw them?

Not sure what one would call them but is is certainly not orthogonal. Maybe simi-cyclic coordinate system?

 

[anuttarasammyak]

Axes are x and y as I wrote x- y- directions of velocity in my post #2.
In xy coordinate, $P(x_p,0)$. The contact point on the slope $C(x_C,y_C)$ in xy axes coordinate is
$$x_C=x_P+R\phi \cos \beta+x_{C0}$$
$$y_C=-R\phi \sin \beta+y_{C0}$$
where $(x_{C0}, y_{C0})$ is initial position of C when t=0, $\phi=0$. Then the center of cylinder $Q(x_Q,y_Q)$ are given as
$$x_Q=x_C+ R\sin \beta$$
$$y_Q=y_C+R\cos \beta$$
by adding constants. All these things are in works of xy coordinates. You get Lagrangian from these Cartesian expressions. Once you got Lagrangian written by $x_P$ and $\phi$ , forget about Cartesian coordinates and go into analytics of $x_P$ and $\phi$ by Lagrange equation, which is the merit of analytical mechanics.

 

[haruspex]

x vs x_p coordinate. I don't think that x is the same as x_p

You are right…
As I understand your working, (x, y) is the location of the centre of the cylinder in the coordinates as diagrammed.
If $(\bar x, \bar y)$ is the same point in your $(\hat{\bar x}, \hat{\bar y})$ coordinates then $x\hat x+y\hat y=\bar x\hat{\bar x}+\bar y\hat{\bar y}$.
Also, $\hat{\bar x}=\hat x$, $\hat{\bar y}=\hat x\cos(\beta)-\hat y\sin(\beta)$, whence $x=\bar x+\bar y\cos(\beta)$, $y=-\bar y\sin(\beta)$.

This choice of coordinates effectively considers the motion of the cylinder as the same motion as the block ($\dot x_P=\dot{\bar x}$) plus a motion down the slope of the block ($\dot{\bar y}=R\dot\phi$).