Classical mechanics: forces on a pendulum

[REVIANNA]

Homework Statement

[/B]
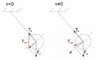
A simple pendulum is pulled sideways from the equilibrium position and then released.
I figured this part out -
Immediately after the pendulum is released, the net force acting on it is directed:
it is perpendicular to the string
(I REASONED THAT THE DIRECTION OF ACCELERATION(PERPENDICULAR TO THE STRING) IS THE DIRECTION OF THE NET FORCE)

but next part to this question of the question says
"My answer to part 1 is justified because:"
AND the answer is " The centripetal acceleration is zero"

I don't understand how the centripetal force is zero?
if it is zero why the circular motion? Does tangential force alone causes it?

 

[stockzahn]

I don't understand how the centripetal force is zero?
if it is zero why the circular motion? Does tangential force alone causes it?

The centripetal force is not zero. If you stand on the floor you don't move downwards... does that mean the gravitational force is zero?

 

[REVIANNA]

The centripetal force is not zero

sorry I meant to say how the CENTRIPETAL ACCELERATION (NOT FORCE) is zero?(as the ans says)
coz the pendulum is after all tracing a semi -CIRCULAR arc.

 

[stockzahn]

You are right, the centripetal acceleration is not zero. I'd say a badly expressed answer. I think the answer should say "the radial velocity is zero" to point out that the distance of the mass from the center is constant. But as the centripetal acceleration points in radial direction and the radial velocity is zero, I suppose the expressions got mixed up.

 

[REVIANNA]

this makes me think
if net force perpendicular to the string mgsin(theta) causes Tangential acceleration then what causes Centripetal acceleration (which causes change in direction) as the net force along the string is zero?

 

[stockzahn]

If the string would be cut (when the pendulum is already in motion), the mass would proceed linearly in tangential direction. The string forces the mass to change the direction of the velocity - due to the inertia the tension in the string increases. Now the net force gets a component in radial direction.

As you wrote in the statement:

Immediately after the pendulum is released, the net force acting on it is directed: [...]

EDIT: I should have read the statement properly in the first place. In the first moment, immediately after the pendulum is released, there is no centripetal acceleration - sorry, my bad.

 

[GoodPost]

Hmm ... well, but we know that the centripetal acceleration, by definition, depends on the velocity, right?

 

[GoodPost]

Is the velocity the same everywhere?

 

[REVIANNA]

due to the inertia the tension in the string increases. Now the net force gets a component in radial direction.

okay this means that immediately after letting the pendulum go the net force is perpendicular to the string (completely tangential ) but as the pendulum goes on- tension increases (as it is a self adjusting force like normal force) such that the acceleration and net force vector have both tangential and radial components which would cause a change in magnitude and direction of the velocity vector respectively.

 

[REVIANNA]

Is the velocity the same everywhere?

no it changes both in magnitude and direction.That's why we are talking about acceleration and net force. Remember Newton's 1st law constant velocity (same speed in a stg line) requires no force at all.

 

[REVIANNA]

Hmm ... well, but we know that the centripetal acceleration, by definition, depends on the velocity, right?

you are right about centripetal acceleration being v^2/r. but as @stockzahn said the centripetal acceleration is zero immediately after the pendulum is released when the velocity is zero too.after that the centripetal force has a certain magnitude.

 

[GoodPost]

Exactly! So at the moment when we just release the ball, the net force along the tension axes is :
T - mg*cos(theta) = m*ac = m*(v^2/r) = m*(0) = 0

And now the force "mg*sin(theta)" will cause the ball to move and so causing the velocity to increase. Hence, ac is changing too (increasing or decreasing) due to the change in velocity.

As a result, the net force along the tension axes is not zero anymore! (centripetal force is not zero)

Good Luck!
G.P.

 

[stockzahn]

okay this means that immediately after letting the pendulum go the net force is perpendicular to the string (completely tangential ) but as the pendulum goes on- tension increases (as it is a self adjusting force like normal force) such that the acceleration and net force vector have both tangential and radial components which would cause a change in magnitude and direction of the velocity vector respectively.

Yes, that's it

 

[REVIANNA]

@stockzahn Thank you so much !