- #1
Aidyan
- 182
- 14
The below experimental setup is of the sort one finds frequently discussed in the delayed choice quantum eraser (QE) experiments, such as that of Kim et al. (https://arxiv.org/abs/quant-ph/9903047) I extracted only the essential part I'm wondering about and did not find a satisfying answer in other threads.
To recapitulate, on the left a light source (say a laser), then the usual double slits, in front of each slit there is a polarizer which filters the horizontal component (H) and vertical component (V) for slit S1 and S2 respectively. A Glan-Thompson prism splits the two orthogonally polarized beams and sends the H-pol. beam towards mirror M1 and the V-pol. beam towards mirror M2. These then are reflected or transmitted at beamsplitter BS, which recombines the two beams and is supposed to erase the 'which-way' information. The question is: what will we observe on screen 1 and 2?
My first instinctive answer was that to think of an interference pattern, just as in the two slits experiment, eventually with on one screen displaying a fringe- on the other an anti-fringe interference pattern (note that the two sides at the BS are not symmetric: the beam going towards screen 1 is a superposition of a reflected H-pol. and transmitted V-pol. beam, whereas the opposite is true for the beam going towards screen 2). This is also what the literature on QE seems to suggest (I say 'suggest' because they did not use screens in place, only detectors).
However, later I could not convince myself that this is the case. Because, taking a more classical EM wave theory approach, one must not forget that two mutually orthogonal polarized light beams going through double slits do not produce interference fringes (just google 'interference of polarized light'). This will also lead to a different interference pattern than that we are accustomed with in the conventional Young experiment, and can be captured by modifying the intensity function as follows:
##I\left(\delta \phi,\delta\theta\right)= I_1+I_2+2 \sqrt{I_1 I_2} \, (cos{\delta (\phi))} \cdot c o s{(\delta\theta)}##,
where ##I_1## and ##I_2## are the intensities from slit 1 and 2 respectively, ##\delta \phi## is the usual angular phase path difference of the beams that modulates the interference term and ##\theta## is the relative separation angle between the polarization vectors of the two beams. This latter term is usually omitted in analyzing the standard double slit experiment because if no polarizer is in place ##\delta\theta=0##. If however ##\delta\theta=\pi/2## the entire interference term is canceled and only the two intensities ##I_1## and ##I_2## remain, that is, we have no interference fringes. So, should we therefore expect to see only the usual Gaussian probability function on both screens?
On the other side, are we not always told that if the photons 'which-way' information is erased we should expect the interference fringes to reappear?
So, I'm confused. There seems to me a contradiction between the classical and quantum perspective. Where did I get it wrong?
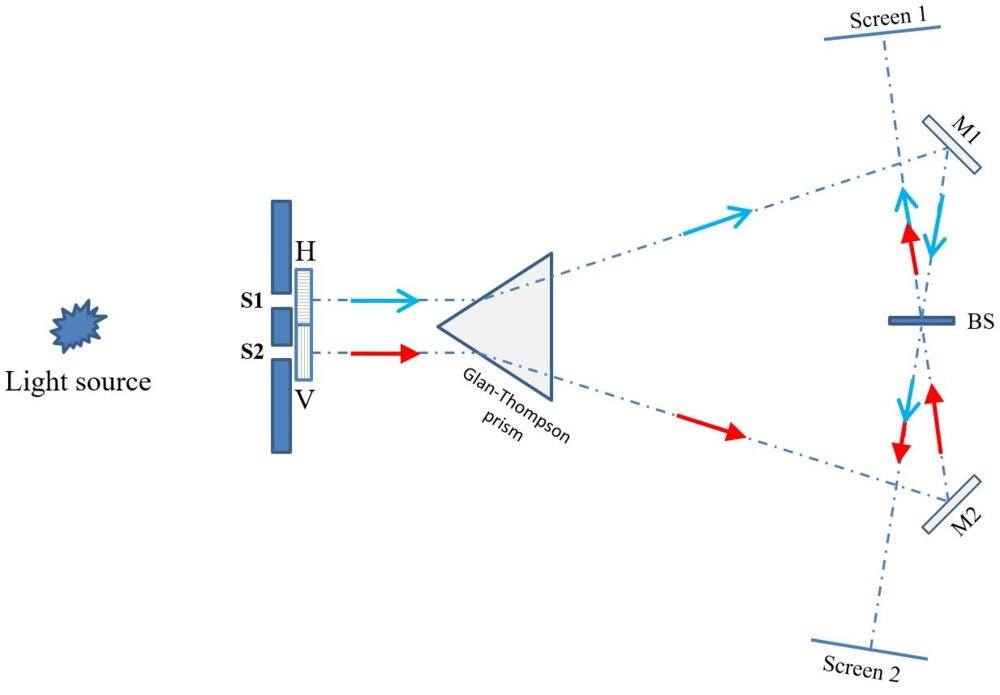
To recapitulate, on the left a light source (say a laser), then the usual double slits, in front of each slit there is a polarizer which filters the horizontal component (H) and vertical component (V) for slit S1 and S2 respectively. A Glan-Thompson prism splits the two orthogonally polarized beams and sends the H-pol. beam towards mirror M1 and the V-pol. beam towards mirror M2. These then are reflected or transmitted at beamsplitter BS, which recombines the two beams and is supposed to erase the 'which-way' information. The question is: what will we observe on screen 1 and 2?
My first instinctive answer was that to think of an interference pattern, just as in the two slits experiment, eventually with on one screen displaying a fringe- on the other an anti-fringe interference pattern (note that the two sides at the BS are not symmetric: the beam going towards screen 1 is a superposition of a reflected H-pol. and transmitted V-pol. beam, whereas the opposite is true for the beam going towards screen 2). This is also what the literature on QE seems to suggest (I say 'suggest' because they did not use screens in place, only detectors).
However, later I could not convince myself that this is the case. Because, taking a more classical EM wave theory approach, one must not forget that two mutually orthogonal polarized light beams going through double slits do not produce interference fringes (just google 'interference of polarized light'). This will also lead to a different interference pattern than that we are accustomed with in the conventional Young experiment, and can be captured by modifying the intensity function as follows:
##I\left(\delta \phi,\delta\theta\right)= I_1+I_2+2 \sqrt{I_1 I_2} \, (cos{\delta (\phi))} \cdot c o s{(\delta\theta)}##,
where ##I_1## and ##I_2## are the intensities from slit 1 and 2 respectively, ##\delta \phi## is the usual angular phase path difference of the beams that modulates the interference term and ##\theta## is the relative separation angle between the polarization vectors of the two beams. This latter term is usually omitted in analyzing the standard double slit experiment because if no polarizer is in place ##\delta\theta=0##. If however ##\delta\theta=\pi/2## the entire interference term is canceled and only the two intensities ##I_1## and ##I_2## remain, that is, we have no interference fringes. So, should we therefore expect to see only the usual Gaussian probability function on both screens?
On the other side, are we not always told that if the photons 'which-way' information is erased we should expect the interference fringes to reappear?
So, I'm confused. There seems to me a contradiction between the classical and quantum perspective. Where did I get it wrong?