- #1
ATroelstein
- 15
- 0
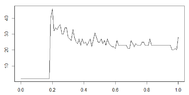
I have generated the graph shown below and now would like to describe it at a high-level according to the curved nature of the plotted line. Besides simply stating observations such as the exponential growth at approximately x = 0.19, is there a classification or term for the shape of the curve this line makes? Thank you.
View attachment 1096
View attachment 1096