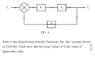
- #1
Jason-Li
- 119
- 14
- Homework Statement
- Derive the closed loop transfer function for the system shown in FIGURE 4 and show that for large values of G the value of Vo/Vi approaches unity.
- Relevant Equations
- Transfer Functions used
Hi all Physics Forum User, I am again coming to you to ask for help.
For the above question I can't make sense of how a larger G will cause Vo/Vi to approach 1. For this I'll call Vo=V and Vi=I
As can be seen from the control loop
B = A*H and V = B*K hence V = A*H*K
Also A = I - C and C=Vo*G therefore A = I - V*G
Then substituting in V =(I-V*G)*HK
Hence Vo/Vi = (H*K) / (1+H*K*G)
Increasing G in this would have an opposite effect on making Vo/Vi approach unity.
Can anyone shed any light on this?