- #1
JD_PM
- 1,131
- 158
- TL;DR Summary
- I am studying the derivation of the polarized cross-section for Compton Scattering by electrons (i.e. both initial and final electron and photon states are set) from Mandl & Shaw (M&S)'s QFT book (chapter 8, section 8.6) and vanhees71's Manuscript (6.5.1 Compton Scattering).
I have specific questions, but let's first give context.
Initially we have an electron with momentum ##p=(E, \vec p)## and spin state ##u_r (\vec p)## and a photon with momentum ##k=(\omega, \vec k)## and polarization state ##\epsilon_s (\vec k)##.
Finally we have ##p'=(E', \vec p')##, ##u_r' (\vec p')##, ##k'=(\omega', \vec k')##, ##\epsilon_s' (\vec k')##
I understand that the differential-cross section for Compton Scattering by electrons is given by (more details here):
$$\frac{d \sigma}{d \Omega} = \frac{m^2 \omega'}{16 \pi^2 E E' \omega v_{rel}} \Big[ \Big( \frac{\partial(E'+\omega')}{\partial \omega'}\Big)_{\theta \phi} \Big]^{-1} |\mathscr{M}|^2 \ \ \ \ (1)$$
Where ##(\theta, \phi)## are the polar angles of ##\vec k'## and ##d \Omega = \sin \theta d \theta d \phi## is the corresponding infinitesimal solid angle. We take ##\vec k## as the polar coordinate axis, so that ##\vec k \cdot \vec k' = \omega \omega' \cos \theta## (where ##\cos \theta## arises due to the definition of the dot product).
Conservation of momentum gives
$$p+k=p'+k' \ \ \ \ (2)$$
The Feynman Amplitudes associated to these two figures are as follows
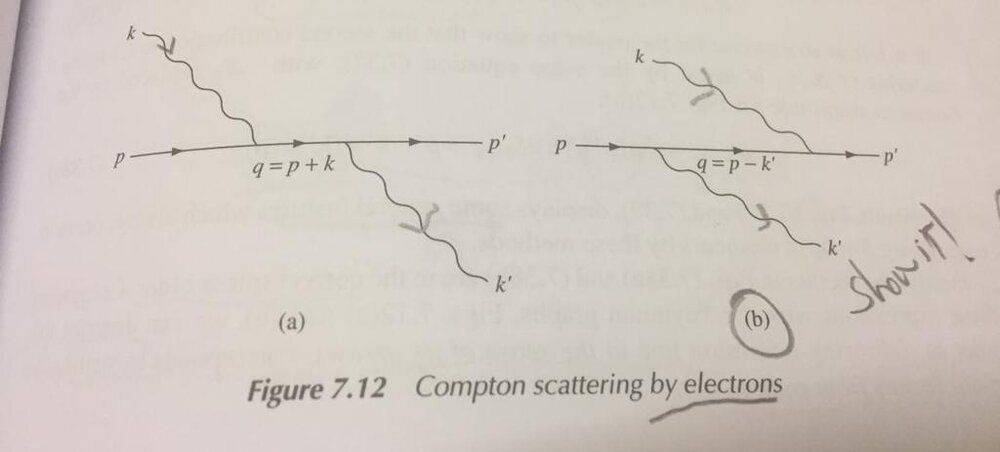 $$\mathscr{M}=\mathscr{M}_a+\mathscr{M}_b \ \ \ \ (3)$$
$$\mathscr{M}=\mathscr{M}_a+\mathscr{M}_b \ \ \ \ (3)$$
$$\mathscr{M}_a = -i e^2 \frac{\bar u' \gamma^{\mu} \epsilon_{\mu}' (\gamma^{\mu} f_{\mu}+m) \gamma^{\mu} \epsilon_{\mu} u}{2(pk)}, \ \ \ \ \mathscr{M}_b = i e^2 \frac{\bar u' \gamma^{\mu} \epsilon_{\mu}' (\gamma^{\mu} g_{\mu}+m) \gamma^{\mu} \epsilon_{\mu}' u}{2(pk')} \ \ \ \ (4)$$
Where
$$f:=p+k, \ \ \ \ g:=p-k'$$
Eq. (3) is manifestly covariant and must be equivalent (I did not check it out myself though) to vanhees71's equation (6.128).
Experimentally the photon beam (usually) aims at a target of nearly stationary electrons. We now move to the LAB frame, which means that we have
$$p=(m, 0, 0, 0), \ \ \ \ \vec p' = \vec k - \vec k' \ \ \ \ (5)$$
Thus the energy-momentum equation yields
$$E' = \Big( m^2 + (\vec k - \vec k')^2 \Big)^{1/2} = \Big( m^2 + \omega^2 + \omega'^2 - 2\omega\omega' \cos\theta \Big)^{1/2} \ \ \ \ (6)$$
Mandl & Shaw asserted that from equation (2) we can get
$$pk=p'k+k'k=pk'+k'k \ \ \ \ (7)$$
And that Eq. (7) reduces to
$$\omega' = \frac{m \omega}{m+\omega(1-\cos\theta)} \ \ \ \ (8)$$
From Eq. (6) we get
$$\Big( \frac{\partial(E'+\omega')}{\partial \omega'}\Big)_{\theta \phi} = \frac{m \omega}{E' \omega'} \ \ \ \ (9)$$
Then, plugging back into (1) we get the differential cross section in the LAB frame
$$\Big( \frac{d \sigma}{d \Omega}\Big)_{LAB} = \frac{1}{(4 \pi)^2} \Big( \frac{\omega'}{\omega}\Big)^2 |\mathscr{M}|^2 \ \ \ \ (10)$$
These are my questions:
1) Where's Eq. (7) coming from?
M&S stated it comes from equation (2). However, I solve for ##p## and multiply (on the right) by ##k## but don't get (7)
$$pk = p'k+k'k-kk \neq p'k+k'k$$
$$pk = p'k+k'k-kk \neq pk'+k'k$$
2) Where's Eq. (8) coming from?
Let's assume Eq. (7); thus we have (recalling the definition of the 4 inner product ##p_1 \cdot p_2 = E_1 E_2 - \vec p_1 \cdot \vec p_2##)
$$(m\omega, 0)=(m \omega + \omega' \omega, -(\vec k - \vec k') \cdot \vec k - \vec k' \cdot \vec k)=(m \omega' + \omega' \omega, \vec k' \cdot \vec k)$$
Simplifying a bit we get
$$(m\omega, 0)=(m \omega + \omega' \omega, -\vec k \cdot \vec k )=(m \omega' + \omega' \omega, \vec k' \cdot \vec k)$$
Recalling that ##\vec k \cdot \vec k' = \omega \omega' \cos \theta## we get
$$(m\omega, 0)=(m \omega + \omega' \omega, -\omega^2 \cos \theta )=(m \omega' + \omega' \omega, \omega' \omega \cos \theta)$$
So we end up with these two equations
$$m\omega=m\omega+\omega'\omega=m\omega'+\omega'\omega \ \ \ \ (*)$$
$$\omega' \cos \theta=-\omega \cos \theta \ \ \ \ (**)$$
Mmm Eq. (*) is trivial so it tells us nothing interesting, but what can we say about ##(\omega'+\omega)\cos\theta=0##? Does it lead to Eq. (8)?
3) I am not getting Eq. 9
It has to be simply about taking the partial derivative but I am making a mistake I do not see...
$$\frac{\partial}{\partial \omega'} (E'+\omega') = \frac{\partial}{\partial \omega'} \Big[ \Big( m^2 + \omega^2 + \omega'^2 - 2\omega\omega' \cos\theta \Big)^{1/2}+\omega' \Big] = \frac{\omega'-\omega \cos \theta}{\sqrt{m^2 + \omega^2 + \omega'^2 - 2\omega\omega' \cos\theta}}+1=\frac{\omega'-\omega \cos \theta+E}{E} \neq \frac{m \omega}{E' \omega'}$$
Any help is appreciated.
Thank you
Initially we have an electron with momentum ##p=(E, \vec p)## and spin state ##u_r (\vec p)## and a photon with momentum ##k=(\omega, \vec k)## and polarization state ##\epsilon_s (\vec k)##.
Finally we have ##p'=(E', \vec p')##, ##u_r' (\vec p')##, ##k'=(\omega', \vec k')##, ##\epsilon_s' (\vec k')##
I understand that the differential-cross section for Compton Scattering by electrons is given by (more details here):
$$\frac{d \sigma}{d \Omega} = \frac{m^2 \omega'}{16 \pi^2 E E' \omega v_{rel}} \Big[ \Big( \frac{\partial(E'+\omega')}{\partial \omega'}\Big)_{\theta \phi} \Big]^{-1} |\mathscr{M}|^2 \ \ \ \ (1)$$
Where ##(\theta, \phi)## are the polar angles of ##\vec k'## and ##d \Omega = \sin \theta d \theta d \phi## is the corresponding infinitesimal solid angle. We take ##\vec k## as the polar coordinate axis, so that ##\vec k \cdot \vec k' = \omega \omega' \cos \theta## (where ##\cos \theta## arises due to the definition of the dot product).
Conservation of momentum gives
$$p+k=p'+k' \ \ \ \ (2)$$
The Feynman Amplitudes associated to these two figures are as follows
$$\mathscr{M}_a = -i e^2 \frac{\bar u' \gamma^{\mu} \epsilon_{\mu}' (\gamma^{\mu} f_{\mu}+m) \gamma^{\mu} \epsilon_{\mu} u}{2(pk)}, \ \ \ \ \mathscr{M}_b = i e^2 \frac{\bar u' \gamma^{\mu} \epsilon_{\mu}' (\gamma^{\mu} g_{\mu}+m) \gamma^{\mu} \epsilon_{\mu}' u}{2(pk')} \ \ \ \ (4)$$
Where
$$f:=p+k, \ \ \ \ g:=p-k'$$
Eq. (3) is manifestly covariant and must be equivalent (I did not check it out myself though) to vanhees71's equation (6.128).
Experimentally the photon beam (usually) aims at a target of nearly stationary electrons. We now move to the LAB frame, which means that we have
$$p=(m, 0, 0, 0), \ \ \ \ \vec p' = \vec k - \vec k' \ \ \ \ (5)$$
Thus the energy-momentum equation yields
$$E' = \Big( m^2 + (\vec k - \vec k')^2 \Big)^{1/2} = \Big( m^2 + \omega^2 + \omega'^2 - 2\omega\omega' \cos\theta \Big)^{1/2} \ \ \ \ (6)$$
Mandl & Shaw asserted that from equation (2) we can get
$$pk=p'k+k'k=pk'+k'k \ \ \ \ (7)$$
And that Eq. (7) reduces to
$$\omega' = \frac{m \omega}{m+\omega(1-\cos\theta)} \ \ \ \ (8)$$
From Eq. (6) we get
$$\Big( \frac{\partial(E'+\omega')}{\partial \omega'}\Big)_{\theta \phi} = \frac{m \omega}{E' \omega'} \ \ \ \ (9)$$
Then, plugging back into (1) we get the differential cross section in the LAB frame
$$\Big( \frac{d \sigma}{d \Omega}\Big)_{LAB} = \frac{1}{(4 \pi)^2} \Big( \frac{\omega'}{\omega}\Big)^2 |\mathscr{M}|^2 \ \ \ \ (10)$$
These are my questions:
1) Where's Eq. (7) coming from?
M&S stated it comes from equation (2). However, I solve for ##p## and multiply (on the right) by ##k## but don't get (7)
$$pk = p'k+k'k-kk \neq p'k+k'k$$
$$pk = p'k+k'k-kk \neq pk'+k'k$$
2) Where's Eq. (8) coming from?
Let's assume Eq. (7); thus we have (recalling the definition of the 4 inner product ##p_1 \cdot p_2 = E_1 E_2 - \vec p_1 \cdot \vec p_2##)
$$(m\omega, 0)=(m \omega + \omega' \omega, -(\vec k - \vec k') \cdot \vec k - \vec k' \cdot \vec k)=(m \omega' + \omega' \omega, \vec k' \cdot \vec k)$$
Simplifying a bit we get
$$(m\omega, 0)=(m \omega + \omega' \omega, -\vec k \cdot \vec k )=(m \omega' + \omega' \omega, \vec k' \cdot \vec k)$$
Recalling that ##\vec k \cdot \vec k' = \omega \omega' \cos \theta## we get
$$(m\omega, 0)=(m \omega + \omega' \omega, -\omega^2 \cos \theta )=(m \omega' + \omega' \omega, \omega' \omega \cos \theta)$$
So we end up with these two equations
$$m\omega=m\omega+\omega'\omega=m\omega'+\omega'\omega \ \ \ \ (*)$$
$$\omega' \cos \theta=-\omega \cos \theta \ \ \ \ (**)$$
Mmm Eq. (*) is trivial so it tells us nothing interesting, but what can we say about ##(\omega'+\omega)\cos\theta=0##? Does it lead to Eq. (8)?
3) I am not getting Eq. 9
It has to be simply about taking the partial derivative but I am making a mistake I do not see...
$$\frac{\partial}{\partial \omega'} (E'+\omega') = \frac{\partial}{\partial \omega'} \Big[ \Big( m^2 + \omega^2 + \omega'^2 - 2\omega\omega' \cos\theta \Big)^{1/2}+\omega' \Big] = \frac{\omega'-\omega \cos \theta}{\sqrt{m^2 + \omega^2 + \omega'^2 - 2\omega\omega' \cos\theta}}+1=\frac{\omega'-\omega \cos \theta+E}{E} \neq \frac{m \omega}{E' \omega'}$$
Any help is appreciated.
Thank you
Last edited: