Einstein44
- 125
- 31
I was looking for a way to calculate the friction arising from the axle and wheel of a standard lab cart. I came across this research paper: https://www.usna.edu/Users/physics/mungan/_files/documents/Publications/PhysEd4.pdf
That derived the following equation for the coefficient of rolling friction:
$$\mu _{r}\approx \frac{D+kr}{R}$$
for what the variables stand can be seen on the diagram shown in the article (it would be too difficult to explain this with words).
Now my problem is that I had never heard of a such thing and want able to find much on the internet that explained it in detail. I wasn't able to follow the derivation exactly, but I think some people here will find it easier to follow.
My question is: is this really a correct indicator of the friction for a cart moving down a ramp, and how can this be used to find the frictional Force? Can you just simply use the same approach as for dynamic friction for instance? (just multiplying it by the Normal Force?)
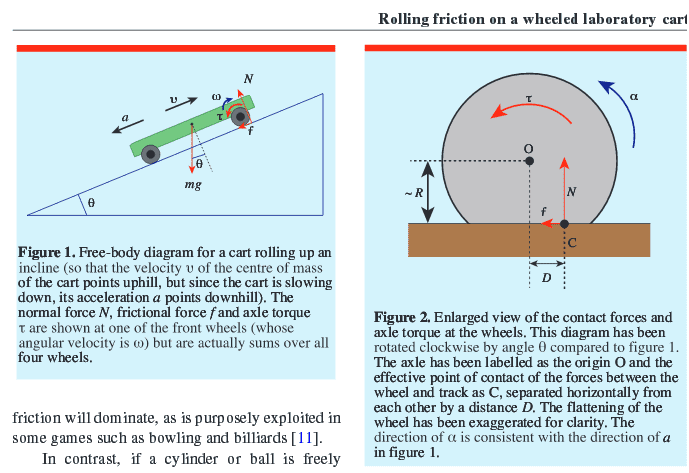
That derived the following equation for the coefficient of rolling friction:
$$\mu _{r}\approx \frac{D+kr}{R}$$
for what the variables stand can be seen on the diagram shown in the article (it would be too difficult to explain this with words).
Now my problem is that I had never heard of a such thing and want able to find much on the internet that explained it in detail. I wasn't able to follow the derivation exactly, but I think some people here will find it easier to follow.
My question is: is this really a correct indicator of the friction for a cart moving down a ramp, and how can this be used to find the frictional Force? Can you just simply use the same approach as for dynamic friction for instance? (just multiplying it by the Normal Force?)