Collection of Bizarre Math Theorems and Conjectures

[mathbalarka]

Hi, MHB.

I have decided set up a thread on collection of most bizarre statements of mathematical problems. I have thought of some, and I hope other MHB members would add some - it would be fun! The statement of the problem you are going to post should be

1) Very weirdly related to the reality
2) Must seem unapproachable in terms of mathematical language at a glance
3) Very tough to solve even if described mathematically
4) A little famous in mathematical community.

Here are my choices :

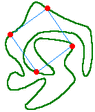
Theorem (Toeplitz, partially solved by Stromquist) : Every simple closed curve that you can draw by hand will pass through the corners of some square.

Theorem (Brouwer, solved by Hadamard & Brouwer) : You have two identical pieces of paper with the same picture printed on them. Put one flat on a table and the other one you crumple up without tearing it and place it on top of the first one, then there is some point in the picture on the crumpled-up page that is directly above the same point on the bottom page.

Balarka
.

 

[alyafey22]

Theorem (Toeplitz, partially solved by Stromquist) : Every simple closed curve that you can draw by hand will pass through the corners of some square.

.

Interesting ! , what do you mean by partially solved ?

 

[mathbalarka]

Interesting ! , what do you mean by partially solved ?

Stromquist's theorem says settles the matter for nice curves, but several simple and closed curves has fractal-like behavior, so surely, this is not enough.

Here's a picture of a particularly nasty curve with an inscribed square :

View attachment 1620

Have fun twiddling with this nice little conjecture! Who knows, you might even solve it!

NOTE : The conjecture has been proved for triangles, and shown that the vertices of all the triangles that is similar to the given is dense in any nice simple closed curve.

 

[mathbalarka]

Here's another :

Theroem (Plücker) : The number of real bitangents of any quartic curve is either 28, 16 or smaller than 9.

A construction of 28 by Trott (7 given, others can be derived from symmetry) :

 

[ModusPonens]

This is one of the most fascinating ideas for a topic I've seen! So far living to the expectation of what it could be. Thanks. :)

Here is my modest contribution, which possibly doesn't fit all criteria:

A Banach Space X with dim (X) = $\infty$ doesn't have a countable vector space basis.

 

[mathbalarka]

Here is my modest contribution, which possibly doesn't fit all criteria

Although your problem doesn't satisfy (1), I certainly do accept theorems realted to countability, or decidability.

Here are some others;

Theorem (Jaffe & Ruberman) : Any sextic surface on P³ have at most 65 double points.

A construction by Barth :

Theorem (Banach & Tarski) : Given a solid ball in 3‑dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces which can then be put back together in a different way to yield two identical copies of the original ball.

Theorem (Poincaré, solved by Perelman) : In a compact 3-dimensional surface without boundary, if every loop can be tightened to a certain point in the surface, then the surface is homeomorphic (i.e., similar) to a 3-sphere.

 

[alyafey22]

Most of the theorems seem to be connected to Algebraic topology here is one that I see interesting

Brouwer fixed-point theorem: Every continuous mapping \(\displaystyle f : D^n \to D^n\) has a fixed pint.

 

[mathbalarka]

Most of the theorems seem to be connected to Algebraic topology here is one that I see interesting

Brouwer fixed-point theorem: Every continuous mapping \(\displaystyle f : D^n \to D^n\) has a fixed pint.

Heh :D, a similar version of this was given by me in the first post to satisfy condition (1) :

Theorem (Brouwer, solved by Hadamard & Brouwer) : You have two identical pieces of paper with the same picture printed on them. Put one flat on a table and the other one you crumple up without tearing it and place it on top of the first one, then there is some point in the picture on the crumpled-up page that is directly above the same point on the bottom page.

 

[Opalg]

The hairy ball theorem: you cannot comb a spherical dog in such a way that its fur lies smoothly flat at each point.

 

[mathbalarka]

The hairy ball theorem: you cannot comb a spherical dog in such a way that its fur lies smoothly flat at each point.

I definitely missed this one - very nice!

 

[I like Serena]

A coast line has infinite length. -Benoit Mandelbrot
Its dimension is something between that of a curve and a surface.
A specific example is the Koch curve with dimension $\log_3 4 \approx 1.26186$.

 

[mathbalarka]

A specific example is the Koch curve with dimension $\log_3 4 \approx 1.26186$.

Indeed a very good example. This post made me think of a conjecture :

The Hausdorff dimension of a certain Weierstrass function \(\displaystyle \sum_{k=1}^{\infty} \frac{\sin (2^k x)}{\sqrt{2}^k}\) is exactly 3/2.

Also, thinking of fractals, the Banach-Tarski paradox holds for a 3-banach tree (and the construction is particularly of interest).

 

[DreamWeaver]

What a great idea for a thread, Mathbalarka! Well played... (Muscle)This one doesn't quite fit your criteria, but I think/hope it's odd enough to fit in well here.The Hairy Ball Theorem (no giggles, please! )

When considering a tennis ball, or other hairy ball, if one attempts to comb all of the hairs in a particular direction, this attempt will be successful in the general sense, except for a tufty patch at one (arbitrary) pole, and a bald patch at another.

Now, considering the weather systems (ie wind currents) of planet Earth to be analogous to hairs on a ball being swept in arbitrary directions, the Hairy Ball Theorem tells us that - at all times - there must be at least two 'weather singularities', ie cyclones, hurricanes, etc, somewhere, on our beloved planet... AT. ALL. TIMES...

Not bad weather prediction for a hairy ball... (Heidy)

 

[alyafey22]

There exists no retraction between a disk and a circle.

 

[mathbalarka]

Theorem (Riemann) : If an infinite series is conditionally convergent, then a permutation exists between the terms which, after summed, converges or diverges.

A consequence of this can be made so that (1) is satisfied : The product of all real numbers without 0 converges to -1. (*)

(*) Note how the order is not specified at this point!

PS : The theorem is called Riemann rearrangement theorem.

Balarka
.

 

[Opalg]

Theorem (Riemann) : If an infinite series is conditionally convergent, then a permutation exists between the terms which, after summed, converges or diverges.

Even more bizarre than that, if an infinite series is conditionally convergent, then the terms can be rearranged to make the series converge to any sum that you care to choose.

For example, the series $1 - \frac12 + \frac13 - \frac14 + \frac15 - \frac16 + \ldots$ converges (conditionally) to $\ln2$. But by rearranging the terms you can make it converge to $\ln3$, or to $-999$, or to $\pi^{17}$, or to anything else you choose.

The proof is a lot easier than you might expect. Notice that the odd-numbered terms are all positive, and form a divergent series. The even-numbered terms are all negative, and also form a divergent series. To rearrange the series so that it converges to the limit $l$, start by taking the positive terms $1+\frac13 + \frac15 + \ldots$, stopping as soon as their sum exceeds $l$. Then take sufficiently many of the negative terms $-\frac12 - \frac14 - \frac16 - \ldots$ until the sum dips down below $l$. Then take some more of the positive terms until the sum goes back up above $l$, and so on. That way, you force the rearranged series to converge to $l$.

 

[mathbalarka]

Even more bizarre than that, if an infinite series is conditionally convergent, then the terms can be rearranged to make the series converge to any sum that you care to choose.

Indeed. $S = 1 - 1 + 1 - 1 + 1 - 1 + ...$ can be made to converge to pretty much anything in $\mathbb{Z}$, and of course 1/2. This is what I at least have off the top of my head.

 

[DreamWeaver]

Great thread! Keep 'em coming... (heart)

 

[Shobhit]

The Riemann hypothesis (in the language of Integrals and Series ):

$$\int_{0}^{\infty}\frac{(1-12t^2)}{(1+4t^2)^3}\int_{1/2}^{\infty}\log|\zeta(\sigma+it)|~d\sigma ~dt=\frac{\pi(3-\gamma)}{32}$$

where $\gamma$ denotes the Euler Mascheroni Constant.

Reference: V. V. Volchkov, On an equality equivalent to the Riemann hypothesis

 

[mathbalarka]

Yes, I knew that form of RH, it's particularly nice. (although not much of a way to approach the conjecture :p)

Okay, here's one from number theory :

Theorem (Tanaka, as a disproof of Polya's conjecture) : The smallest number n for which most of the number smaller than n has even number of prime factors is n = 906150257.

 

[mathbalarka]

Conjecture (Jaeger) : Every bridgeless graph has a cycle-continuous mapping to the Petersen graph.

And, oh, how did I forgot these two :

Theorem (Proved by Appel & Haken) The regions of a map can be colored using at most four colors so that no two adjacent regions have the same color.

Conjecture (McKay, Radziszowski & Exoo) R(5, 5) = 43 where R(a, b) is the least number of vertices of a graph red or blue colored for which a subgraph of a number of vertices or a subgraph of b vertices exists with edges painted entirely red or entirely blue, respectively.

 

[mente oscura]

Hello.

Humble conjecture: "mente oscura".

$$Let \ n \in{N} \ / \ P(n)=n^2-n+41$$

$$Let \ p \in{N} \ / p>1 \ / \ p|P(n)$$

Conjecture:

$$p \geq{41}$$

Regards.

 

[mathbalarka]

The "conjecture" you refer to is proved by Euler a long time ago. See, Lucky numbers of Euler - Wikipedia, the free encyclopedia

I don't think it belongs here as it is not at all "bizarre" and not very hard to prove. In fact, it follows from this theorem : http://mathhelpboards.com/challenge-questions-puzzles-28/prime-generating-polynomials-7618.html.

 

[mente oscura]

The "conjecture" you refer to is proved by Euler a long time ago. See, Lucky numbers of Euler - Wikipedia, the free encyclopedia

I don't think it belongs here as it is not at all "bizarre" and not very hard to prove. In fact, it follows from this theorem : http://mathhelpboards.com/challenge-questions-puzzles-28/prime-generating-polynomials-7618.html.

Thank you very much, for your, always, interesting "post".:)

 

[DreamWeaver]

Just a thought, mind, but since there's been plenty of abstract ideas/theorems on here already, does anyone have any nice visual or geometric ones to share...?

(Hug)

 

[mathbalarka]

Theorem (Schubert) : Every knot can be uniquely expressed as the connected sum of prime knots.

Maybe this?

 

[mathbalarka]

Theorem (Proved by B. Green and T. Tao) : There are arbitrarily large magic squares consisting primes as components.

Thought this version was cool. :D