- #1
I am not a robot
- 1
- 0
Let \(\displaystyle n\in \mathbb{Z}_{>0}\). For every subset \(\displaystyle S\subseteq \left[ n-1\right]\) we define a poset \(\displaystyle P_S=\left([n],\le_{P_S}\right)\) given by the covering relation \(\displaystyle \lessdot\) which is defined as
Clearly, the Hasse diagram of these kind of orderings represents a path with an ordering defined by the corresponding set. For instance if \(\displaystyle n=3\) we have the posets
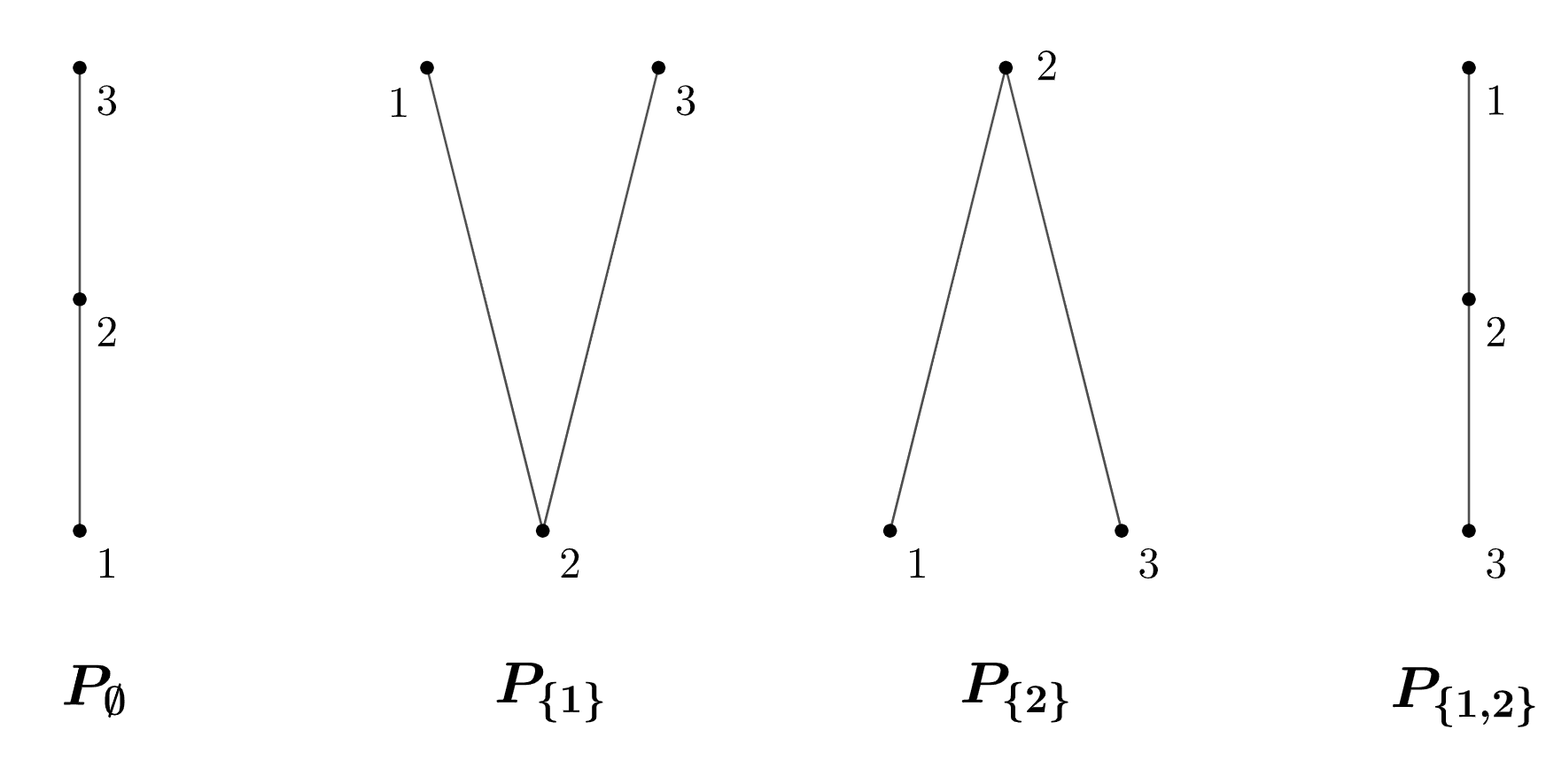
Useful Definitions
- A function \(\displaystyle f\colon P_S\to [m]\) is called order-preserving for \(\displaystyle P_S\), if for any \(\displaystyle x,y\in P_S\)
- We denote with \(\displaystyle \Omega(P_S,m)\) the order polynomial of \(\displaystyle P_S\) for \(\displaystyle m\), i.e.
- For any permutation \(\displaystyle w\in\mathcal{S}_n\) we denote with \(\displaystyle \mathsf{Des}(w)\) the descent set of \(\displaystyle w\), i.e.
The question
We want to calculate, for any given \(\displaystyle m\in\mathbb{Z}_{>0}\) the sum of the order polynomials on the subsets \(\displaystyle S\subseteq[n-1]\), i.e.
It seems that the requested sum is equal to
but I did not manage to show it.----------------------It is not hard to show that the set of all the natural labelings for a given subset \(\displaystyle S\) has the same cardinality as the set of all permutations of \(\displaystyle [n]\) with descent set equal to \(\displaystyle S\), i.e.
It is well known that
I tried to use these facts in order to calculate the requested sum but I failed...I would love some help :)
\(\displaystyle \forall i\in S \qquad i+1\lessdot i \)
\(\displaystyle \forall i\in\left[n-1\right]\setminus S \qquad i\lessdot i+1\)
\(\displaystyle \forall i\in\left[n-1\right]\setminus S \qquad i\lessdot i+1\)
Clearly, the Hasse diagram of these kind of orderings represents a path with an ordering defined by the corresponding set. For instance if \(\displaystyle n=3\) we have the posets
Useful Definitions
- A function \(\displaystyle f\colon P_S\to [m]\) is called order-preserving for \(\displaystyle P_S\), if for any \(\displaystyle x,y\in P_S\)
\(\displaystyle x<_{P_S}y\implies f(x)\le f(y),\)
where \(\displaystyle m\in\mathbb{Z_{>0}}\).- We denote with \(\displaystyle \Omega(P_S,m)\) the order polynomial of \(\displaystyle P_S\) for \(\displaystyle m\), i.e.
\(\displaystyle \Omega(P_S,m)=\#\left\{ f\colon P_S\to [m]\,\mid f\;\; \text{is order-preserving}\right\}\)
- We call an order-preserving bijection \(\displaystyle \omega\colon P_S\to[n]\) natural labeling of \(\displaystyle P_S\).- For any permutation \(\displaystyle w\in\mathcal{S}_n\) we denote with \(\displaystyle \mathsf{Des}(w)\) the descent set of \(\displaystyle w\), i.e.
\(\displaystyle \mathsf{Des}(w)=\left\{ i\in\left[n\right]\mid w\left(i\right)>w\left(i+1\right)\right\} \)
The question
We want to calculate, for any given \(\displaystyle m\in\mathbb{Z}_{>0}\) the sum of the order polynomials on the subsets \(\displaystyle S\subseteq[n-1]\), i.e.
\(\displaystyle \sum_{S\subseteq[n-1]}\Omega\left(P_{S},m\right).\)
My progressIt seems that the requested sum is equal to
m(1+m)^{n-1},
but I did not manage to show it.----------------------It is not hard to show that the set of all the natural labelings for a given subset \(\displaystyle S\) has the same cardinality as the set of all permutations of \(\displaystyle [n]\) with descent set equal to \(\displaystyle S\), i.e.
\(\displaystyle \#\left\{ \omega\colon P_{S}\to[n]\mid\omega\;\text{natural labeling}\right\} =\#\left\{ w\in\mathcal{S}_{n}\mid\mathsf{Des}\left(w\right)=S\right\} .\)
It is well known that
\(\displaystyle \Omega\left(P_{S},m\right)=\sum_{w\in A_{S}}\binom{m+n-\mathsf{des}\left(w\right)-1}{n},\)
where \(\displaystyle A_S\) is the set of permutations that corresponds to the natural labelings of \(\displaystyle P_S\), i.e.\(\displaystyle A_{S}=\left\{ w\in\mathcal{S}_{n}\mid w=\left(\omega\left(1\right),\omega\left(2\right),\dots,\omega\left(n\right)\right)\text{ for some natural labeling }\omega\text{ of }P_{S}\right\}\)
I tried to use these facts in order to calculate the requested sum but I failed...I would love some help :)