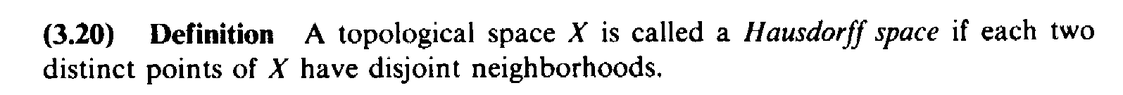Compact Topological Spaces .... Stromberg, Theorem 3.36 .... ....

[Math Amateur]

I am reading Karl R. Stromberg's book: "An Introduction to Classical Real Analysis". ... ...

I am focused on Chapter 3: Limits and Continuity ... ...

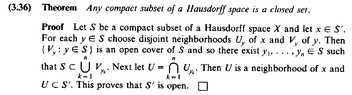
I need help in order to fully understand the proof of Theorem 3.36 on page 102 ... ... Theorem 3.36 and its proof read as follows:

View attachment 9134

In the above proof by Stromberg we read the following:

" ... ...Next let $$U = \bigcap_{ k = 1 }^n U_{ y_k }$$. Then $$U$$ is a neighbourhood of $$x$$ and $$U \subset S'$$ ... "
My question is as follows:

It seems plausible that $$U \subset S'$$ ... ...

... ... BUT ... ...

... how would we demonstrate rigorously that $$U \subset S'$$ ... ... ?

(Note that $$S'$$ is $$S$$ complement ...)

Help will be much appreciated ... ...

Peter=================================================================================The above post mentions Hausdorff spaces ... so I am providing access to Stromberg's definition of a Hausdorff space ... as follows:
View attachment 9135I believe it may be helpful to MHB readers to have access to some of Stromberg's terminology and notation associated with topological spaces ... so I am providig access to the same ... as follows:
View attachment 9136

Hope that helps ... ...

Peter

 

[castor28]

Hi Peter,

If $U\not\subset S'$, there is an element $u\in U\cap S$. Since the $V_y$ cover $S$, $u\in V_{y_n}$ for some $n$.

On the other hand, as $u\in U$, $u\in U_{y_k}$ for all $k$. In particular, $u\in U_{y_n}$ and this contradicts the fact that $U_{y_n}$ and $V_{y_n}$ are disjoint.

Note that the fact that $S$ is compact is essential (the theorem would obviously be false otherwise); do you see why?

 

[Opalg]

For each $k$, $U_{y_k}$ is disjoint from $U_{y_k}$. Therefore $U$ is disjoint from $V_{y_k}$ (because $U\subseteq U_{y_k}$). That holds for each $k$, and so $U$ is disjoint from $$ \bigcup_{k=1}^n V_{y_k} = V$$. But $S\subseteq V$, so $U$ is disjoint from $S$, in other words $U\subseteq S'$.Edit. Sorry, I didn't see that castor28 had already replied.

 

[Math Amateur]

Hi Peter,

If $U\not\subset S'$, there is an element $u\in U\cap S$. Since the $V_y$ cover $S$, $u\in V_{y_n}$ for some $n$.

On the other hand, as $u\in U$, $u\in U_{y_k}$ for all $k$. In particular, $u\in U_{y_n}$ and this contradicts the fact that $U_{y_n}$ and $V_{y_n}$ are disjoint.

Note that the fact that $S$ is compact is essential (the theorem would obviously be false otherwise); do you see why?

Thanks castor28 ... ...

You write:

" ... ... Note that the fact that $S$ is compact is essential (the theorem would obviously be false otherwise); do you see why? ... ... "Intriguing question ... Not sure I see why ... can you help ...

Mind you ... the argument given depends on having a finite subcover of S which arises via compactness ... but do we really need a finite cover ... would an infinite cover work with slightly amended arguments ... again ... I am not sure ...Peter

- - - Updated - - -

For each $k$, $U_{y_k}$ is disjoint from $U_{y_k}$. Therefore $U$ is disjoint from $V_{y_k}$ (because $U\subseteq U_{y_k}$). That holds for each $k$, and so $U$ is disjoint from $$ \bigcup_{k=1}^n V_{y_k} = V$$. But $S\subseteq V$, so $U$ is disjoint from $S$, in other words $U\subseteq S'$.Edit. Sorry, I didn't see that castor28 had already replied.

Thanks for the hep, Opalg ...

Peter

 

[castor28]

Hi Peter,

You need that to ensure that $U$ is a neighborhood of $x$. In a topological space, any union or any finite intersection of open sets is open, but that does not hold for infinite intersections.

For example, in $\mathbb{R}$, the intersection of the open intervals $\{(-x,x)\mid x\ne0\}$ is the singleton $\{0\}$, which is not open.

 

[Math Amateur]

Hi Peter,

You need that to ensure that $U$ is a neighborhood of $x$. In a topological space, any union or any finite intersection of open sets is open, but that does not hold for infinite intersections.

For example, in $\mathbb{R}$, the intersection of the open intervals $\{(-x,x)\mid x\ne0\}$ is the singleton $\{0\}$, which is not open.

Thanks for that really subtle and interesting point, castor28 ...

Peter