Compare rotational inertia of 2 paper cups in 2 diff orientations

[dcmf]

Homework Statement

The objects in (Figure 1) are made of two identical paper cups glued together. Rank the rotational inertias I1, I2, I3, and I4 about the indicated axes. Rank from largest to smallest. To rank items as equivalent, overlap them.

Relevant Equations

thin ring/hollow cylinder about its axis: I = MR^2
thin rod about center: I = (1/12)ML^2
thin rod about end: I = (1/3)ML^2
disk/solid cylinder about its axis: I = (1/2)MR^2
solid sphere about diameter: I = (2/5)MR^2
hollow sphere about diameter: I = (2/3)MR^2

Figure 1:

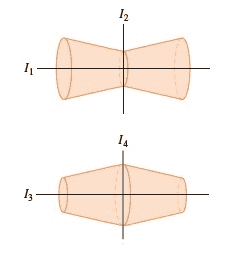
I assume this is a conceptual question regarding the usage of the above inertia equations but the axes are really confusing me. I would imagine that around I1 and I3, you could say that the total inertia is just the sum of all the ring-shaped "slices" of the paper cups (i.e. use the equation I = MR^2). And because the paper cups are identical, their I1 and I3 would therefore be identical.

But I have no idea how to approach the shapes for I2 and I4. Also I'm unsure as to how to make a comparison between all these shapes after I've determined which equation to apply.

 

[Orodruin]

I don’t think this is about actually computing the moments of inertia as much as a conceptual question to argue about their relative sizes.

 

[dcmf]

I don’t think this is about actually computing the moments of inertia as much as a conceptual question to argue about their relative sizes.

I fully agree. I do not plan to compute any of these inertias. However, I'm pretty sure I need to use the inertia equations to compare each situation.

My confusion stems from the nonconventional shape of the glued paper cups (larger radius at the rims, smaller radius at the base) and how to best apply the inertia equations presented in class.

My best guess is that I1 and I3 use I=MR^2 and I2 and I4 use I=(1/12)ML^2 but we are not given any information about the length of the cup (L) relative to the radius (R) - nor the radius at the rim relative to the radius at the base, for that matter. Evidently this information is not necessary, since it was not provided, but I am having trouble seeing how we can make the comparisons without. We were also taught that a greater distance between an object's mass concentration and its axis results in a greater rotational inertia - which I think would help differentiate that I2 > I4. But again, I don't know how to place I1 and I3 relative to I2 and I4.

 

[kuruman]

There are two simple considerations.
1. Symmetry.
2. The more mass you have closer to the axis, the smaller the moment of inertia.

I will not say more for the time being.

 

[dcmf]

I feel like I have considered both, though.

Point 1 suggests that I1 = I3 due to the placement of the axes.
Point 2 suggests that I2 > I4 due to the orientation of the cups.

However I am still having trouble figuring out how to place I1 and I3 relative to I2 and I4 (i.e. I1=I3 > I2 > I4 or I2 > I1=I3 > I4 or I2 > I4 > I1=I3). I assume I am missing something about the application of these concepts.

 

[haruspex]

Point 1 suggests that I1 = I3 due to the placement of the axes.

Not sure how you get that from symmetry. Another principle is additivity: if a body is considered as a rigid combination of two bodies, the MoI of the whole body about a given axis is the sum of the MoIs of the components about the same axis.

Point 2 suggests that I2 > I4 due to the orientation of the cups.

Again, additivity helps.

However I am still having trouble figuring out how to place I1 and I3 relative to I2 and I4

And so you should be. You would need to know the dimensions and do the calculations.
Even if you take the diagrams as roughly accurate, it is hard to say.
I assume the cups are hollow and lidless, but do they have bases? Let's say not.
For $I_1$, the effective overall radius is a little more than the average radius. For $I_2$, it is a bit over half the cup height (horizontal here). Not obvious which is greater.

 

[kuruman]

Not sure how you get that from symmetry.

Take two identical cups and place them on a mirror, one upside down and the other right side up. An object has the same MoI as its mirror image about an axis perpendicular to the plane of the mirror. Additivity says that each cup and its reflection has twice the moment of inertia about the axis of symmetry ($I_1$ or $I_3$) of a single cup.

 

[erobz]

Not obvious which is greater.

I too think they should have exaggerated the dimensions a bit if they meant for it to be objective.

For the record my instincts for the ordering (least to greatest) are $[I_1,I_3], I_4, I_2$.

 

[haruspex]

Take two identical cups and place them on a mirror, one upside down and the other right side up. An object has the same MoI as its mirror image about an axis perpendicular to the plane of the mirror. Additivity says that each cup and its reflection has twice the moment of inertia about the axis of symmetry ($I_1$ or $I_3$) of a single cup.

Yes, I was unclear; I meant from symmetry alone. You have to combine it with additivity.

 

[haruspex]

Having done the algebra, if the end radii are $R_1, R_2$ and the length (cup height) is L then $I_1=I_2$ (or $I_3=I_4$) when
$L^2=\frac{3(R_2+R_1)(R_2^2+R_1^2)}{2(3R_2+R_1)}$

 

[erobz]

Having done the algebra, if the end radii are $R_1, R_2$ and the length (cup height) is L then $I_1=I_2$ (or $I_3=I_4$) when
$L^2=\frac{3(R_2+R_1)(R_2^2+R_1^2)}{2(3R_2+R_1)}$

Did you check to see how plausible these dimensions are from the picture?

 

[haruspex]

Did you check to see how plausible these dimensions are from the picture?

Exercise for the reader.

 

[dcmf]

Hi all, I really appreciate the insight. I think I'm still having a little trouble grasping the rationale behind the ranking but I think I'm going to go find my teacher and ask for further clarifications when she's available later in the week cause I think I've spent far too long on this one problem this weekend haha

Did you check to see how plausible these dimensions are from the picture?

And yes, I will look into it :)