- #1
ajw124
- 1
- 0
I was wondering if anyone could help me with this integral. I've heard of contour integration but I'm unsure of how it would be used for this integral.
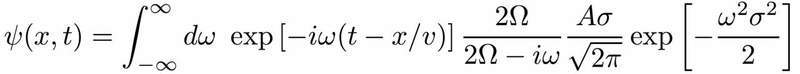
A Fourier Transform Integral is a mathematical operation that converts a function from its original domain (usually time or space) to a representation in the frequency domain.
A Fourier Transform Integral is completed by performing an integration over the function with respect to the variable of interest, typically time or space.
The purpose of completing a Fourier Transform Integral is to analyze the frequency components of a given function and to understand how the function's behavior changes over different frequencies.
A Fourier Transform Integral can be applied to any function that is continuous and has finite energy, including waveforms, signals, and images.
One limitation is that the function must be well-behaved, meaning that it must have a finite number of discontinuities and singularities. Additionally, the function must have finite energy in order for the integral to converge.