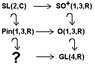- #1
Ruslan_Sharipov
- 104
- 1
Please, how to complete the commutative diagram shown on the following attachment picture?
Attachments
Last edited by a moderator: