Completing the square using algebra tiles

[Gitty]

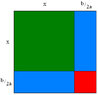
I'm trying to create a square using algebra tiles. The question is x^2 + 4x + 5. I know how to do it without the algebra tiles but I don't know how to do it with the algebra tiles.

Can anyone give me a hand with this?

 

[MarkFL]

Consider the following diagram:

View attachment 5305

In the quadratic:

$$y=x^2+4x+5$$

Let the green square represent $x^2$, which we have, and the 2 blue rectangles each represent $$2x$$ ($x$ by 2), which we also have, and so we see the red square will need to have side lengths of 2, and thus an area of 4, so we can then write:

$$y=\left(x^2+4x+4\right)+1$$

We know the expression within the parentheses represents the entire square, whose sides measure $x+2$, and so we may write:

$$y=(x+2)^2+1$$