- #1
Morto
- 12
- 0
I'm not sure whether to post this in the Mathematics or Physics forums, but I figure this problem is easily reduced to its transformation irrespective of the physics it describes.
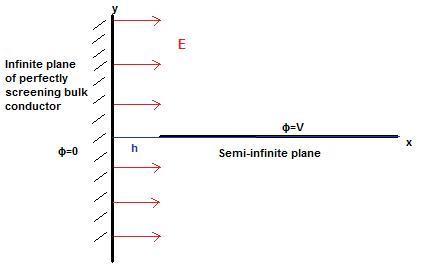
Consider a semi-infinite sheet of (infinitely thin) conductor charged to a potential [tex]V[/tex]. It is placed at a distance [tex]h[/tex] perpendicular to a perfectly screening bulk conductor (so the electric field is always perpendicular to the surface). See the attachment below. I want to investigate the charge density on the surface of both sheets. I'm struggling to determine the transformation that can describe the electrostatic field.
Now, I have calculated a similar problem with a semi-infinite conducting plane paralell to an infinite conducting plane at a distance [tex]h[/tex]
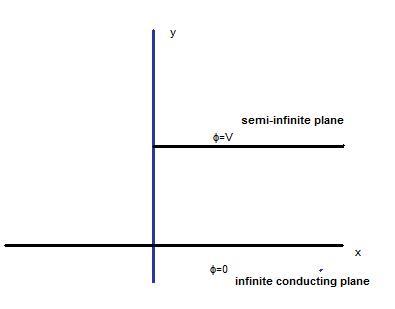
I have transformed it into the upper half-plane (so it looks like a capacitor), and I found the transformation
[tex]
z = h \left( \frac{w}{V} - \frac{1}{\pi} \left(1+ e^{-\frac{\pi w}{V}} \right) \right)
[/tex]
determines this electrostatic field. How can I transform my problem with perpendicular planes into something similar? Can I use this result, with another transformation? Any help would be greatly appreciated.
Consider a semi-infinite sheet of (infinitely thin) conductor charged to a potential [tex]V[/tex]. It is placed at a distance [tex]h[/tex] perpendicular to a perfectly screening bulk conductor (so the electric field is always perpendicular to the surface). See the attachment below. I want to investigate the charge density on the surface of both sheets. I'm struggling to determine the transformation that can describe the electrostatic field.
Now, I have calculated a similar problem with a semi-infinite conducting plane paralell to an infinite conducting plane at a distance [tex]h[/tex]
I have transformed it into the upper half-plane (so it looks like a capacitor), and I found the transformation
[tex]
z = h \left( \frac{w}{V} - \frac{1}{\pi} \left(1+ e^{-\frac{\pi w}{V}} \right) \right)
[/tex]
determines this electrostatic field. How can I transform my problem with perpendicular planes into something similar? Can I use this result, with another transformation? Any help would be greatly appreciated.
Last edited: