Amad27
- 409
- 1
Hello,
Evaluate:
$$\int_{0}^{\infty} \frac{\cos(x)}{x^2 + 1} dx$$
We know that because $f(x)$ is even:$$\int_{0}^{\infty} \frac{\cos(x)}{x^2 + 1} dx = \frac{1}{2} \cdot \int_{-\infty}^{\infty} \frac{\cos(x)}{x^2 + 1} dx$$
Consider a complex function, with $z = x + iy$
$$f(z) = \frac{\cos(z)}{z^2 + 1}$$
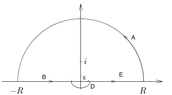
Consider a contour $C$ on the top half of the axis, with top-semi-circle $B$, and the x-axis from $-R \to R$
We will consider:
$$\oint_{C} \frac{\cos(z)}{z^2 + 1} dz$$
Consider $z^2 + 1 = 0 \implies z = \pm i$
But because we consider the top half, only $z = i$ suffices.
$$\text{Res}_{z=i} f(z) = \lim_{z=i} (z-i) \cos(z)\cdot \frac{1}{(z-i)(z+i)}$$
$$= \frac{\cosh(1)}{2i}$$
Which implies due to the Residue theorem:
$$\oint_{C} \frac{\cos(z)}{z^2 + 1} dz = (2\pi i)\cdot \frac{\cosh(1)}{2i} = \pi\cosh(1) $$
Keeping in mind that:
$$\oint_{C} \frac{\cos(z)}{z^2 + 1} dz = \int_{-\infty}^{\infty} \frac{\cos(x)}{x^2 + 1} \,dx + \int_{B} \frac{\cos(z)}{z^2 + 1} dz = \pi\cosh(1)$$
But how do we evaluate:
$$\int_{B} \frac{\cos(z)}{z^2 + 1} dz$$
??
Thanks
Evaluate:
$$\int_{0}^{\infty} \frac{\cos(x)}{x^2 + 1} dx$$
We know that because $f(x)$ is even:$$\int_{0}^{\infty} \frac{\cos(x)}{x^2 + 1} dx = \frac{1}{2} \cdot \int_{-\infty}^{\infty} \frac{\cos(x)}{x^2 + 1} dx$$
Consider a complex function, with $z = x + iy$
$$f(z) = \frac{\cos(z)}{z^2 + 1}$$
Consider a contour $C$ on the top half of the axis, with top-semi-circle $B$, and the x-axis from $-R \to R$
We will consider:
$$\oint_{C} \frac{\cos(z)}{z^2 + 1} dz$$
Consider $z^2 + 1 = 0 \implies z = \pm i$
But because we consider the top half, only $z = i$ suffices.
$$\text{Res}_{z=i} f(z) = \lim_{z=i} (z-i) \cos(z)\cdot \frac{1}{(z-i)(z+i)}$$
$$= \frac{\cosh(1)}{2i}$$
Which implies due to the Residue theorem:
$$\oint_{C} \frac{\cos(z)}{z^2 + 1} dz = (2\pi i)\cdot \frac{\cosh(1)}{2i} = \pi\cosh(1) $$
Keeping in mind that:
$$\oint_{C} \frac{\cos(z)}{z^2 + 1} dz = \int_{-\infty}^{\infty} \frac{\cos(x)}{x^2 + 1} \,dx + \int_{B} \frac{\cos(z)}{z^2 + 1} dz = \pi\cosh(1)$$
But how do we evaluate:
$$\int_{B} \frac{\cos(z)}{z^2 + 1} dz$$
??
Thanks