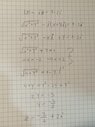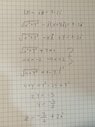Callmelucky
- 144
- 30
- Homework Statement
- Photo of procedure below.
- Relevant Equations
- z= x+yi, |z|=sqrt(x^2 + y^2), i^2=-1
Here is my attempt(photo below), but somehow the solution in the textbook is z= 2 - (3/2)i, and mine is z=(-3/2) +2i.
Can someone please tell me where I am making a mistake? I suppose it's something with x being part of the real part of the 1st complex number and x being part of an imaginary number of the 1st complex number. But I don't know how to make it right.
Thank you.
Can someone please tell me where I am making a mistake? I suppose it's something with x being part of the real part of the 1st complex number and x being part of an imaginary number of the 1st complex number. But I don't know how to make it right.
Thank you.
Attachments
Last edited: