milkism
- 118
- 15
- Homework Statement
- I need to find the six currents I_i(t) via a system of diff eqs.
- Relevant Equations
- V=IR, Q=CV, etc
The following circuit is:
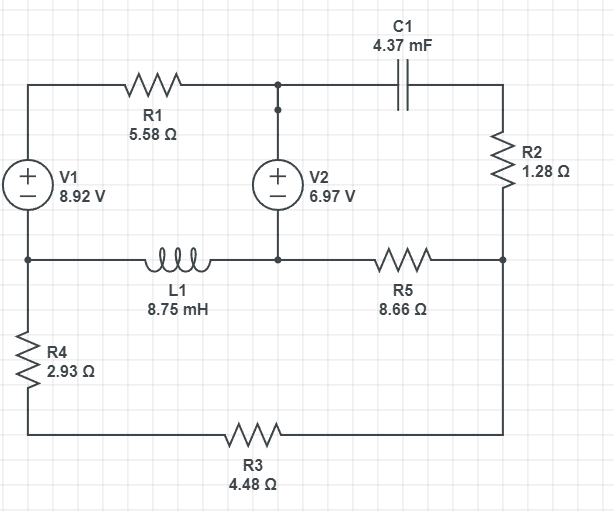
Going clockwise the current ##I_1## goes through resistor ##R_1## and voltage ##V_11##. Current ##I_2## goes through capacitator ##C_1## and ##R_2##.
Current ##I_3## goes through resistors ##R_3## and ##R_4##. Current ##I_4## goes through resistor ##R_5##, but from left to right.
Current ##I_5## goes through the inductor ##L_1## from right to left. And current ##I_6## goes through the voltage ##V_2## from under to above.
I have found the initial values of the currents, when the capacitator acts like a perfect a conductor.
$$I_1 = 0.57$$, $$I_2 = 1.20$$, $$I_3 = 0.57$$, $$I_4 = -0.63$$, $$I_5 = 0$$ and $$I_6 = 0.63$$.
I have gotten these results through these equations:
$$I_2=I_1+ I_6$$, $$V_1 = I_1 ( R_1 + R_3 + R_4) + I_2 * R_2$$, $$V_2 = I_2 * R_2 + I_6 * R_5$$, $$I_1 = I_3$$, $$I_5 = 0$$, $$I_6 = -I_4$$.
For final I have:
$$I_1 = 0.35$$, $$I_2 = 0$$, $$I_3 = 0$$, $$I_4 = 0$$, $$I_5 = 0.35$$ and $$I_6 = -0.35$$.
I have gotten these results through these equations:
$$I_5 + I_3 = I_1$$, $$-I_5 -I_6 - I_4 = 0$$, $$V_1 - V_2 = I_1 * R_1$$, $$V_1 - V_2 = I_1 * R_1 + I_4 * (R_3 + R_4 + R_2)$$, $$I_2 = 0$, $I_4 = I_3$$.
Now the question is, to find the currents at any time. For the top-left branch I got differential equation:
$$V_1 - V_2 = I_1 * R_1 + L \frac{dI_5}{dt}$$ or $$V_1 - V_2 = \frac{dQ_1}{dt} * R_1 + L \frac{d^2Q_5}{d^2t}$$
For top-right branch I got:
$$V_2 = \frac{1}{C} \int I_2 dt + I_2 * R_2 - I_4 * R_5$$ or $$V_2 = \frac{Q_2}{C} + \frac{dQ_2}{dt} R_2 - \frac{dQ_4}{dt} * R_5$$
For the rectangular branch below I got (going clockwise)
$$0=- L \frac{dI_5}{dt} + I_4 * R_5 + I_3 * (R_3 + R_4)$$ or $$0=- L \frac{d^2 Q_5}{d^2t} + \frac{dQ_4}{dt} * R_5 + \frac{dQ_3}{dt} * (R_3 + R_4)$$
I can make an another loop for the outer branch, but you can see each differential equation depends on too many time-dependant variables. So I really have no idea to do!
Going clockwise the current ##I_1## goes through resistor ##R_1## and voltage ##V_11##. Current ##I_2## goes through capacitator ##C_1## and ##R_2##.
Current ##I_3## goes through resistors ##R_3## and ##R_4##. Current ##I_4## goes through resistor ##R_5##, but from left to right.
Current ##I_5## goes through the inductor ##L_1## from right to left. And current ##I_6## goes through the voltage ##V_2## from under to above.
I have found the initial values of the currents, when the capacitator acts like a perfect a conductor.
$$I_1 = 0.57$$, $$I_2 = 1.20$$, $$I_3 = 0.57$$, $$I_4 = -0.63$$, $$I_5 = 0$$ and $$I_6 = 0.63$$.
I have gotten these results through these equations:
$$I_2=I_1+ I_6$$, $$V_1 = I_1 ( R_1 + R_3 + R_4) + I_2 * R_2$$, $$V_2 = I_2 * R_2 + I_6 * R_5$$, $$I_1 = I_3$$, $$I_5 = 0$$, $$I_6 = -I_4$$.
For final I have:
$$I_1 = 0.35$$, $$I_2 = 0$$, $$I_3 = 0$$, $$I_4 = 0$$, $$I_5 = 0.35$$ and $$I_6 = -0.35$$.
I have gotten these results through these equations:
$$I_5 + I_3 = I_1$$, $$-I_5 -I_6 - I_4 = 0$$, $$V_1 - V_2 = I_1 * R_1$$, $$V_1 - V_2 = I_1 * R_1 + I_4 * (R_3 + R_4 + R_2)$$, $$I_2 = 0$, $I_4 = I_3$$.
Now the question is, to find the currents at any time. For the top-left branch I got differential equation:
$$V_1 - V_2 = I_1 * R_1 + L \frac{dI_5}{dt}$$ or $$V_1 - V_2 = \frac{dQ_1}{dt} * R_1 + L \frac{d^2Q_5}{d^2t}$$
For top-right branch I got:
$$V_2 = \frac{1}{C} \int I_2 dt + I_2 * R_2 - I_4 * R_5$$ or $$V_2 = \frac{Q_2}{C} + \frac{dQ_2}{dt} R_2 - \frac{dQ_4}{dt} * R_5$$
For the rectangular branch below I got (going clockwise)
$$0=- L \frac{dI_5}{dt} + I_4 * R_5 + I_3 * (R_3 + R_4)$$ or $$0=- L \frac{d^2 Q_5}{d^2t} + \frac{dQ_4}{dt} * R_5 + \frac{dQ_3}{dt} * (R_3 + R_4)$$
I can make an another loop for the outer branch, but you can see each differential equation depends on too many time-dependant variables. So I really have no idea to do!
Last edited by a moderator: