- #1
yucheng
- 232
- 57
I refer to the website below (for more information):
http://www1.lasalle.edu/~blum/p106wks/pl106_Pendulum.htm#:~:text=The forces acting on the,the tension of the string.&text=The net radial force leads,is v2/r.)
P.S. I'll insert my specific questions in the following paragraphs in this format: {{Q(reference number):}}.
P.S.S I'll use the xy coordinate system (horizontal and vertical), also the radial and tangential coordinate system.
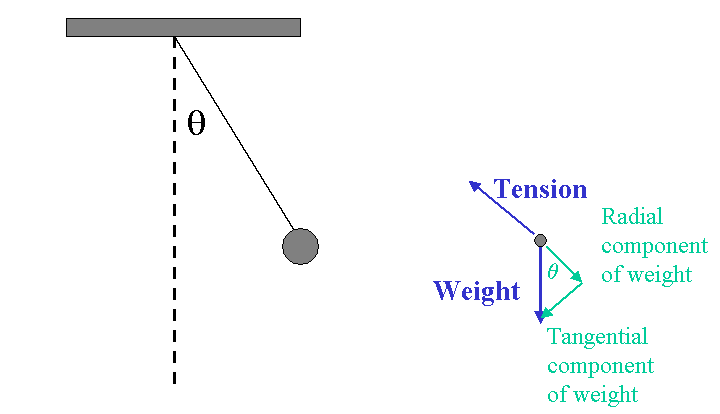
I am referring to the diagram above. Resolving weight into its components, the following equation was given: $$T-mg\cos\theta=ma_{radial}\tag1$$ I was wondering why is the equation true? Let me try by resolving the vector for tension. $$T_y=T\cos\theta \tag2$$ $$T_y=T\sin\theta \tag3$$ Let's assme $$T-mg\cos\theta>0$$, as if it is zero, this means that the $$weight > T$$ and the string will break. {{Q1: Is this reasoning acceptable?}}
Now, let's backtrack a bit and change the way we approached the problem. Instead of resolving weight into its components, we equate ##\tag1## with weight because otherwise, the string will break if ##w>(2)##, and the pendulum bob will not remain in circular motion if there is a component along the vertical axis ##w<(2)## {{Q2: Is this reasoning acceptable?}}. Does this mean that $$T_x=a_{radial}$$, given that the pendulum only moves along the circle in a plane, thus the change in direction is only caused by ##T_x## which is in the same plane? Well, at least that's what my textbook tells me.
Back to our original question, on equation ## (1)##, and given our reasoning on why (1) must be greater than 0, this means we can further resolve (1) into its components? Suppose we equate (1) with ##T"##, however, ##T'## does have a vertical component. The reason being there is still the tangential component of weight, and thus a vertical component of weight which (1) does not take into account. Considering our argument above how the ##a_{radial}## does not have a vertical component, how is ##T'=ma_{radial}##? {{Q3}}
http://www1.lasalle.edu/~blum/p106wks/pl106_Pendulum.htm#:~:text=The forces acting on the,the tension of the string.&text=The net radial force leads,is v2/r.)
P.S. I'll insert my specific questions in the following paragraphs in this format: {{Q(reference number):}}.
P.S.S I'll use the xy coordinate system (horizontal and vertical), also the radial and tangential coordinate system.
I am referring to the diagram above. Resolving weight into its components, the following equation was given: $$T-mg\cos\theta=ma_{radial}\tag1$$ I was wondering why is the equation true? Let me try by resolving the vector for tension. $$T_y=T\cos\theta \tag2$$ $$T_y=T\sin\theta \tag3$$ Let's assme $$T-mg\cos\theta>0$$, as if it is zero, this means that the $$weight > T$$ and the string will break. {{Q1: Is this reasoning acceptable?}}
Now, let's backtrack a bit and change the way we approached the problem. Instead of resolving weight into its components, we equate ##\tag1## with weight because otherwise, the string will break if ##w>(2)##, and the pendulum bob will not remain in circular motion if there is a component along the vertical axis ##w<(2)## {{Q2: Is this reasoning acceptable?}}. Does this mean that $$T_x=a_{radial}$$, given that the pendulum only moves along the circle in a plane, thus the change in direction is only caused by ##T_x## which is in the same plane? Well, at least that's what my textbook tells me.
Back to our original question, on equation ## (1)##, and given our reasoning on why (1) must be greater than 0, this means we can further resolve (1) into its components? Suppose we equate (1) with ##T"##, however, ##T'## does have a vertical component. The reason being there is still the tangential component of weight, and thus a vertical component of weight which (1) does not take into account. Considering our argument above how the ##a_{radial}## does not have a vertical component, how is ##T'=ma_{radial}##? {{Q3}}
Last edited: