Components of vector derivative

[PFuser1232]

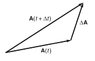
In the book "Introduction to Mechanics" by K&K, an increment of a generic time-varying vector is split into two components, $\Delta \vec{A} _{\perp}$ and $\Delta \vec{A}_{\parallel}$.
Their magnitudes are approximated by:
$$A \Delta \theta$$
and
$$\Delta A$$
respectively. (Where $\Delta \theta$ is the angle between $\vec{A}(t)$ and $\vec{A}(t + \Delta t)$)

Now, I understand why the parallel component of the increment is approximated by $\Delta A$, it's because:

$$|\Delta \vec{A}_{\parallel}| = |\vec{A}(t + \Delta t)| cos(\Delta \theta) - |\vec{A}(t)| ≈ |\vec{A}(t + \Delta t)| - |\vec{A}(t)| = \Delta A$$

for small angles. However, I can't understand how the other approximation is obtained (when changes in magnitude and direction are occurring simultaneously, that is).

My second question:

To find the magnitudes of the derivatives of the vector components, we divide each of the expressions I mentioned above by $\Delta t$, and we take the limit as $\Delta t$ approaches zero. Why did we have to approximate the magnitudes (using the small angle approximation) if we were going to take the limit as $\Delta t$ approaches 0 anyway? Would it make a difference if we were to use the actual equations with strict equality that hold for any angle, big or small, and then take the limit as $\Delta t$ approaches zero?

 

[jedishrfu]

For small angles the slope at sin(0) is one and so the sin(x) can be approximated as x.

 

[PFuser1232]

For small angles the slope at sin(0) is one and so the sin(x) can be approximated as x.

I understand. It's the $A$ part that's confusing me. Using simple trigonometry, the length of the opposite side is $|\vec{A}(t + \Delta t)| sin(\Delta \theta)$.
But isn't $A$ the length of the initial vector? This is why I'm confused.
Had the derivation been for a case of pure rotation with no change in magnitude, it would've been clearer because the magnitude of the (vector) function would've been equal at both times.

 

[jedishrfu]

Yes but aren't the vectors about equal for very small t.

 

[PFuser1232]

Yes but aren't the vectors about equal for very small t.

So what we're doing here is really coming up with approximations for a small change in time, not just change in angle. These approximations become exact when we take the derivative. Right?

 

[PeroK]

So what we're doing here is really coming up with approximations for a small change in time, not just change in angle. These approximations become exact when we take the derivative. Right?

There is another way to do it, if you're not happy with these approximations:

$\frac{\Delta \vec{A} _{\perp}}{A + \Delta \vec{A}_{\parallel}} = tan\Delta \theta$

$\Delta \vec{A} _{\perp} = (A + \Delta \vec{A}_{\parallel}) tan\Delta \theta$

This is exact. Now, if you take the limit, the first term on the RHS becomes $A\frac{d\theta}{dt}$ (since the limit of $\frac{tan(\theta)}{\theta} = 1$.

And the limit of the second term is zero, as you have the product of small terms.

Maybe you can fill in the gaps and find an "exact" derivation for the parallel component.

 

[Redbelly98]

A Δθ can be thought of as using the arc-length formula to approximate the tangential component.

 

[PFuser1232]

There is another way to do it, if you're not happy with these approximations:

$\frac{\Delta \vec{A} _{\perp}}{A + \Delta \vec{A}_{\parallel}} = tan\Delta \theta$

$\Delta \vec{A} _{\perp} = (A + \Delta \vec{A}_{\parallel}) tan\Delta \theta$

This is exact. Now, if you take the limit, the first term on the RHS becomes $A\frac{d\theta}{dt}$ (since the limit of $\frac{tan(\theta)}{\theta} = 1$.

And the limit of the second term is zero, as you have the product of small terms.

Maybe you can fill in the gaps and find an "exact" derivation for the parallel component.

Thanks. This is much better than the method using approximations. I found the limit for the parallel component. This was very helpful!
Is it always possible to avoid approximations in physics derivations that involve calculus (like the one above), or will I be forced to make approximations once in a while?