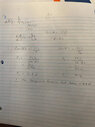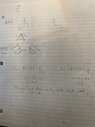Compression Q&A: Answers to Common Questions

[hofner]

Homework Statement

First time posting, really stuck on the question below and any help would be greatly appreciated. Thanks in advance.

3. Forces can also be applied by compressing or tensing a rigid object such as a beam. Two beams support a 4.0-kg pail of water above an open well, as shown in Fig. 7.13.
a) How much compression force is exerted on each beam by the
water pail?
b) What outward force do the two beams exert on the well’s
wall?
(Fig 7.13 is a round well 1.3m wide with a pail suspended above the well from two beams leaning against eachother in a triangle shape 1.9m high from the top of the well to the point at the top of the two beams)

Relevant Equations

Force=mass x gravity

 

[berkeman]

Welcome to PF.

Can you post a better image of your work? And if you could type your math equations into the Edit window (preferably using LaTeX), that would be a big help. I'm not able to read your attachment so far...

 

[hofner]

 

[berkeman]

That helps some, thanks. Can you post the figure that was given with the problem? It seems like it's two inclined beams at different angles supporting a pail of water in the middle?

And as I mentioned, it is a lot easier for us to help if you post your work using LaTeX. Check out the "LaTeX Guide" link below the Edit window.

 

[hofner]

 

[hofner]

I hope that helps! Thank again

 

[berkeman]

It does help some.

I think you are using a mostly correct approach for part (a), but it looks like you didn't divide the total force in half to find the compressive force in each of the two beams? (again, it's still hard for me to read your improved pictures).

For me, I take the total weight of the bucket and divide that in half since there are two supporting beams that are symmetrical. I also divide by the cos() of the angle of the beams, since that goes from divide-by-1 for vertical beams to divide-by-zero (a big number) for horizontal beams.

$$F_{beam} = \frac{mg}{2cos(18.89)} = \frac{4kg * 9.8\frac{m}{s^2}}{2cos(18.89)} = 20.72N$$

So I got half your answer for (a), but I think you just forgot to divide by two since there are two symmetric beams?

 

[hofner]

Wow! Ok thanks for that!

 

[berkeman]

You're welcome. The weird thing is that my LaTeX is not rendering correctly for me (after I told you to use it, sheesh). I'll keep trying to figure out why, but hopefully you can decode what I posted.

 

[hofner]

Lol. We shall try thanks again.

 

[berkeman]

Okay, I fixed my LaTeX. I had a misplaced brace "}". See how easy it is to use LaTeX?

 

[haruspex]

The problem is a little easier if you solve it in the other order.
The vertical component of the compression is obvious, so you can find the horizontal component by taking moments about the end point of a beam; no trig required.
Then you just need Pythagoras to find the total compressive force.

In my experience, the great majority of mechanics problems in which angles are implied by lengths can be solved without ever calculating the angles. You usually just need the trig functions of the angles, but here you do not even need those.