MHB Compute Derivative Using First Principles - MathLoveR's Question

[MarkFL]

Here is the question:

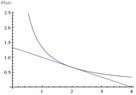
Calculus Question ... Please HELP?

For the function f(x) = 4/3x

a) Using the definition of derivative (limits) to compute f'(3)
b) Use the result of part (a) to find an equation of the line tangent to the curve y = f(x) at the point for which x = 2

Here is a link to the question:

Calculus Question ... Please HELP? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Hello MaThLoVeR,

We are given:

$$f(x)=\frac{4}{3x}$$

a) To compute the derivative of $f$ using first principles, we use:

$$f'(x)\equiv\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$$

Using the given function definition, we have:

$$f'(x)=\lim_{h\to0}=\frac{\frac{4}{3(x+h)}-\frac{4}{3x}}{h}$$

In the numerator of the expression, let's combine the two terms by getting a common denominator:

$$f'(x)=\lim_{h\to0}=\frac{\frac{4(3x)}{3(x+h)(3x)}-\frac{4(3(x+h)}{3x(3(x+h))}}{h}$$

$$f'(x)=\lim_{h\to0}=\frac{4(3x)-4(3(x+h)}{3h(x+h)(3x)}$$

Distribute in the numerator:

$$f'(x)=\lim_{h\to0}=\frac{12x-12x-12h}{3h(x+h)(3x)}$$

Combine like terms:

$$f'(x)=\lim_{h\to0}=\frac{-12h}{3h(x+h)(3x)}$$

Divide out common factors:

$$f'(x)=\lim_{h\to0}=\frac{-4}{(x+h)(3x)}=-\frac{4}{3x^2}$$

Hence:

$$f'(3)=-\frac{4}{3(3)^2}=-\frac{4}{27}$$

b) Now, to find the tangent line where $x=2$, we need a point on the curve:

$$(2,f(2))=\left(2,\frac{2}{3} \right)$$

and we need the slope:

$$m=f'(2)=-\frac{4}{3(2)^2}=-\frac{1}{3}$$

Using the point-slope formula, we find the equation of the tangent line is:

$$y-\frac{2}{3}=-\frac{1}{3}(x-2)$$

Arranging in slope-intercept form, we have:

$$y=-\frac{1}{3}x+\frac{4}{3}$$

Here is a plot of the function and the tangent line:

https://www.physicsforums.com/attachments/826._xfImport

To MaThLoVeR and any other guests viewing this topic, I invite and encourage you to post other calculus problems here in our http://www.mathhelpboards.com/f10/ forum.

Best Regards,

Mark.

 

[Prove It]

Are you sure that [math]\displaystyle f(x) = \frac{4}{3x}[/math] and not [math]\displaystyle \frac{4}{3}x[/math]?

 

[MarkFL]

Are you sure that [math]\displaystyle f(x) = \frac{4}{3x}[/math] and not [math]\displaystyle \frac{4}{3}x[/math]?

No, in fact I am not sure since bracketing symbols were not used, so I made a guess as to what was intended. (Bandit)

Also, the interpretation I used is a somewhat more interesting problem. :D

And a tangent line to a linear function seemed to be a bit strange.(Rofl)