Compute Force f from A, B & C Coordinates

  • Thread starter ktiniatros
  • Start date
  • Tags
    Force
In summary, to compute the force f, you need to find the coordinates of D, which can be determined by using the coordinates of A, B, and C. The segments AB and CD are parallel, so D can be found by multiplying the slope of AB by an arbitrary value of x. This will give the coordinates (x, tan(θ)*x) for D. The size of the square where the force is applied does not matter, as it is considered a point.
  • #1
ktiniatros
2
0
Hi,

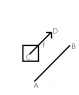
I got a little rusty in the basics.. Need to compute the following force f.

I know the coordinates of A, B and C. Segments AB and CD are parallel. So I need to find to compute the coordinates D of the force f.PS: Don't mind of the size of the square, where the force is applied. I consider it as a spot, I don't care if it has size.
 

Attachments

  • force.png
    force.png
    1.3 KB · Views: 470
Last edited:
Physics news on Phys.org
  • #2
OK, I found it. I am just writing it here for future reference for whoever has the same questrion..

Let's say that x and y are the coordinates of D. Then with some x, the y will be slope of AB multiplied by x. Or the tangent of the angle θ that AB makes with x-axis multiplied with x. So, in order to have such a force, you need a couple of (x,tan(θ)*x). You can set the value of x as big as you force f norm want to be.
 

FAQ: Compute Force f from A, B & C Coordinates

What is the formula for computing force from A, B, and C coordinates?

The formula for computing force from A, B, and C coordinates is F = (B - A) x (C - A), where A, B, and C are vectors representing the coordinates in three dimensions.

How do I determine the direction of the force from A, B, and C coordinates?

The direction of the force can be determined by using the right hand rule. Place your right hand with your fingers pointing in the direction of vector B - A. Then, curl your fingers towards vector C - A. Your thumb will point in the direction of the force.

What are the units of force when computing from A, B, and C coordinates?

The units of force will depend on the units of the coordinates used. For example, if the coordinates are in meters, then the force will be in Newtons (N).

Can this formula be applied to any number of coordinates?

Yes, this formula can be applied to any number of coordinates. However, for simplicity, it is typically used for computing force in three dimensions.

What assumptions are made when using this formula to compute force?

This formula assumes that the forces acting on the object are in equilibrium, meaning that the net force is equal to zero. It also assumes that the object is rigid and that the forces are acting at specific points in space represented by the coordinates.

Similar threads

Where on a rigid body is a resultant force applied?
Replies
11
Views
819
B Liquid Flow Calculation out of a pressurized tank
Replies
3
Views
2K
Equilibrium of a Non-concurrent force system
Replies
8
Views
1K
B How does hovering and constant climbing differ?
Replies
8
Views
2K
I Forces Between 2 large conductors
Replies
3
Views
1K
Force exerted by one molecule on container wall
Replies
1
Views
6K
To what extent does this system behave as a pendulum?
Replies
1
Views
448
Engineering Solve Force at C: Magnitude & Direction | Help Needed
Replies
2
Views
1K
A Is this solution for interstellar travel viable?
Replies
3
Views
1K
B Clarification of coordinate fictitious forces
Replies
29
Views
2K

Hot Threads

Recent Insights

Back
Top