Compute # of Coins for Tray Inner Rim: Examples

[Gianz]

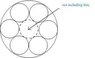
Given the radius of the tray and the uniform radius of coins, how can we compute for the number of coins that can fit in the inner rim (not the whole tray) of the tray? (see attachment...)
Ex1.
Radius of tray -> 6
Radius of coin -> 2
Ans. 6 coins of size 2 will fit the inner rim of a tray of size 6.
Ex2.
Radius of tray -> 8
Radius of coin -> 5
Ans. 1 coin of size 5 will fit the inner rim of a tray of size 8.
Ex3.
Radius of tray -> 4
Radius of coin -> 6
Ans. Coin cannot fit in tray.

 

[Ygggdrasil]

See https://en.wikipedia.org/wiki/Circle_packing