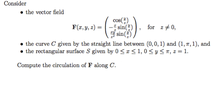Compute the circulation of F along C

[Uniman]

View attachment 417
Hi,
This is my first post. So if I made any mistakes that is the way I asked the questions, kindly let me know.

The work done so far

Circulation:

C {0,0,1} to {1, pi,1}

C eq: {y=pi*x, z=1}

dr={dx, pi*dx, 0}
F={cos(y/z), -x/z*sin(y/z),xy/z^2*sin(y/z)}

F.dr = -dx [dot product and simplified]

Integral[F.dr]{0 t01} = -1

Am I in right track?

 

[Fantini]

Welcome to MHB, Uniman! For future reference and searches later, I believe you should type out the question using LaTeX. It will make it easier for all of us to read and discuss your approach. :D

Last but not least, this looks like a multivariable calculus question. Perhaps it belongs in the Calculus sub-forum. (Nod)

Adjust your http://www.mathhelpboards.com/f16/compute-downwards-flux-f-2170/ accordingly! ;)

 

[Uniman]

Latex? Is it a software available online...Sorry I post these two threads in the wrong section. Am I able to move this thread...
Waiting for the experts to check my answers. By the way this forum looks great...

 

[Jameson]

Hi Uniman,

Welcome to MHB! :)

You can read up on Latex here but in short it's a way to output nice looking equations which are difficult to write otherwise.

For example \frac{x^2+3x-2}{\sqrt{2x^2-11}} outputs \(\displaystyle \frac{x^2+3x-2}{\sqrt{2x^2-11}}\). We have a forum dedicated to Latex which you can find http://www.mathhelpboards.com/f26/.

I am not sure where this thread belongs so I'll ask one of the moderators to move it to a new place if needed. Sorry I can't help you myself but rest assured that you should be getting some help soon.

Jameson

 

[CellCoree]

Hi there,

Based on the information you provided, it seems like you are on the right track in calculating the circulation of F along C. The integral you have set up is correct and you have correctly used the dot product to simplify the calculation. However, it is always a good idea to double check your work and make sure all the units and dimensions match up. Also, it would be helpful to provide more context and background information on what you are trying to solve and what the values of t and t0 represent. Overall, keep up the good work and don't hesitate to reach out for further clarification or assistance. Best of luck!