Computer simulation of geologic processes using multidimensional functions

[GPundergrad]

Hello all, this is my first topic here at PF, though I have been using this site as a homework aid for quite a while. Just to clarify, this problem is NOT a homework problem.

I have been attempting to create a MOD for the 3D lego-like indy game called minecraft. Minecraft features a procedurally generated fractal terrain which makes for interesting and engaging gameplay through use of perlin simplex noise. For most players, the terrain generator is sufficient. Ores are generated as random conglomerations of 1m x 1m x 1m blocks dependent only on surface depth, and replace the existing blocks of 'stone' when they are made.

Having a background in geology, minecraft's terrain generator leaves much to be desired. Mountain ranges are the result of a pure fractal process without the regard for faults, rock types, and erosion. I understand that for game programmers it may be overly complex and involved to include geologic principles in their generators.

I approached one of my professors with this idea, and she immediately recommended that I create this mod for my senior thesis. As I am currently a mathematical physics & Earth system science major (my university does not have a geophysics program), this senior thesis, if completed, will hopefully give me a good shot at getting into a decent geophysics graduate program.

I am initially coding the entire generator in Matlab. Once the generator works, I will work on getting the methods to work in minecraft's native java code.

Soo on to the interesting stuff. So far, this is what the generator does:

-1 it creates a 3D matrix (100x100x256) filled with integer values which correspond to the types of material at that x,y,z index

-2 it partially fills in this matrix (we will call this matrixA) with three layers of rock:
* alluvium, which is 10 layers thick
* Metamorphic rock, which is 30 layers thick
* Intrusive igneous rock (aka granite) which is 20 layers thick, with the lowest layer being at the bottom of the map

-3 it uses a 10x10 matrix filled with random values to create an interpolated 2D heightmap which is used to offset the starting elevation of MatrixA
-4 it fills in the space between 'bedrock'/z coordinate index 1 and the bottom of the resulting granite offset so that there are no voids under the terrain.
-5 renders the side and the top of matrixA as cubes colored corresponding to their rock types.

My next step in this mod will be to add kimberlite pipes (it may seem like a weird jump, let's just roll with it for now):(http://en.wikipedia.org/wiki/Volcanic_pipe)

Kimberlite pipes are basically explosion pits from ancient volcanoes which take the form of a steep cone from ~75m wide to 1.5km wide, and are the primary source of natural diamonds.

I would like my world to at this time include an algorithm for producing kimberlite pipes, however I'm not very sure how to do this. Its easy enough to produce a 3d structure of a cone in matrixA, but a perfect cone isn't what I'm going after:

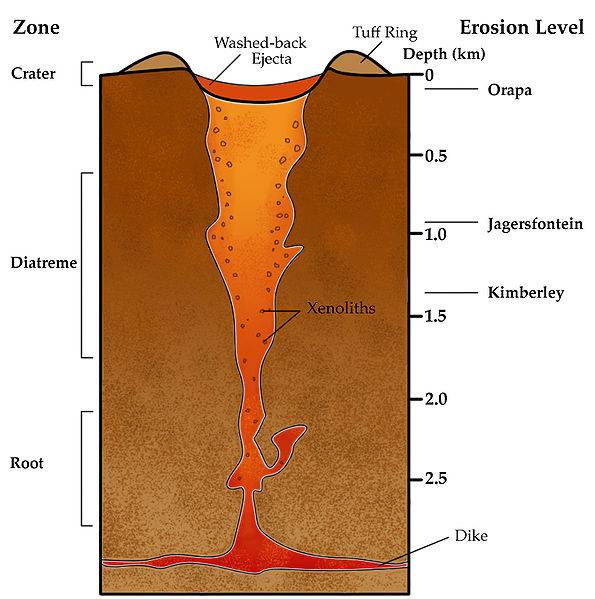
notice that though the diatreme (volcanic pipe) follows a roughly conical shape, there are plenty of wiggles and uncomformities which make for a very organic looking structure. additionally, the whole of the pipe is not necessarily conical in nature:

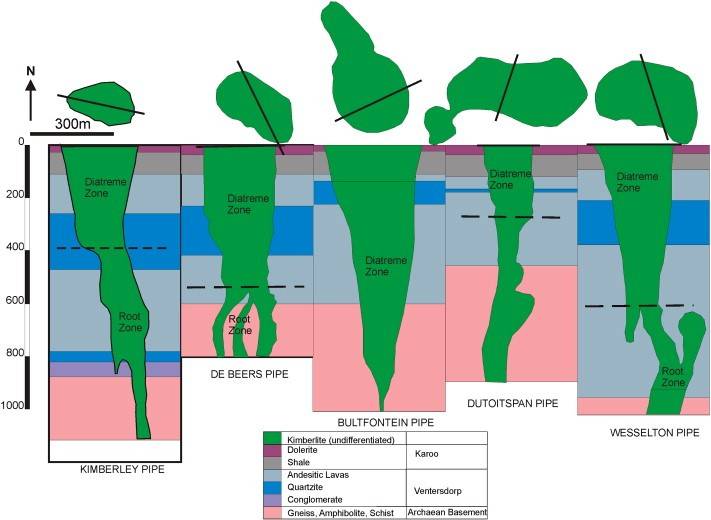
So my question is this: what algorithm should I use to create similar 3D structures inside matrixA without using a simulation of physical processes/without utilizing empirical volumetric data? I need to be mindful of both computational efficiency and the discreet nature of matrixA.

 

[chiro]

Hey GPundergrad and welcome to the forums.

My understanding of your question is that you want to create 3D shapes (or holes) in the context of a volumetric matrix where each element of the 3D matrix corresponds to information about a particular material or absence of one.

The technical term for this is a voxel (volumetric element as opposed to pixel which is picture element) and I would like for you to clarify if I have my thinking right.

If this is right, then the technique you need to use is going to be based on the Bresenham Line Algorithm:

http://en.wikipedia.org/wiki/Bresenham's_line_algorithm

What this algorithm does is basically find the pixels of a line in 2D when it needs to find the best set of pixels to represent the line in a quantized manner.

What you will need to do is to apply the exact same idea to a 3D scenario if I have interpreted your problem correctly.

 

[GPundergrad]

Well in essence that is what I am trying to do, though Matlab has nice functions that make transcribing functions to discreet values easy. My question, and the thing that has been bugging me for a very long time is that I don't know how to create such a function/algorithm that would create a 3D shape similar to many real Kimberlite pipes. In this case, a simple z = x^2 + y^2 just won't cut it.

 

[chiro]

Well in essence that is what I am trying to do, though Matlab has nice functions that make transcribing functions to discreet values easy. My question, and the thing that has been bugging me for a very long time is that I don't know how to create such a function/algorithm that would create a 3D shape similar to many real Kimberlite pipes. In this case, a simple z = x^2 + y^2 just won't cut it.

So which part are you having trouble with? Generating an equation or model for the actual hole structure to cut or creating a method to get the voxel definition of those holes in the same motivation that the above line algorithm does for 2D to get the pixel space definition?

What you should start doing is to implement the algorithm for a single plane and then give another algorithm a number of planes in which it will then generate a set of voxels intersecting those planes.

After this then you can just fill all the voxels on the inside of that object and mark them as holes or whatever material you are thinking of.

The difference between the line algorithm vs the 3D plane implementation is that you will have two independent loops instead of one: you basically do the bresenham algorithm "twice": instead of doing one line you do a series of "line scans" where you trace rays from one side of the plane to the other.

So in short you give it a bunch of planes (i.e. triangles) and you do the bresenham algorithm in the following way:

1. Do two bresenham scans: start at one point A and do it from A to B and A to C. These generate pairs of voxels that you will use to do a loop of line scans.

2. For each pair of points (generated from the first line scans above), do an individual bresnham scan and store all the voxel elements that were found by each scan.

3. Do this for all triangle objects to get a list of all voxels that are used to define the object.

4. Once you have this then fill all interior voxels as holes or whatever data you need.

If you supply planes then you can create as much detail as you want (more planes can be used for more detail) and the algorithm works for any kind of object definition (once you convert it to a bunch of triangles).

 

[GPundergrad]

Ah, I guess I should probably be a little more clear.

I have absolutely no problem defining which voxels I need to 'color in.' When i discovered how to do that, I spent like 6 hrs doing it on all sorts of shapes (it was pretty fun xD).

The problem is I don't have any function to define these initial points. I am not using any predefined datasets or physical simulations to give me coordinates a priori. I don't have any way of defining point 'A', or for that matter B,C,D... etc;

 

[chiro]

Ah, I guess I should probably be a little more clear.

I have absolutely no problem defining which voxels I need to 'color in.' When i discovered how to do that, I spent like 6 hrs doing it on all sorts of shapes (it was pretty fun xD).

The problem is I don't have any function to define these initial points. I am not using any predefined datasets or physical simulations to give me coordinates a priori. I don't have any way of defining point 'A', or for that matter B,C,D... etc;

So do you need a function?

 

[GPundergrad]

After 'meditating' on your answers, I read a bit further and I happened upon the Midpoint Circle Drawing algorithm; http://techforum4u.com/entry.php/816-How-To-Implement-Mid-Point-Circle-Drawing-Algorithm-In-C
I also created a small subroutine in Matlab which creates an interpolated polynomial [pp(ø) = radius from origin]. The polynomial is created like this:

for theta=2*pi/10:2*pi/10:2*pi 
    z(i) = 10 - 2*rand(1);
    t(i) = theta;    
    i = i +1;
end
z(i) = z(1);
t(i) = 0;
pp = spline(t,z);

pp defines the perimeter of the k' diatreme at a specific level. If I can create a succession of these and interpolate points on the perimeters of different planes, I can define the outward surface of the k' diatreme. However, I'm having trouble adapting the Midpoint circle Drawing algorithm to work with a radius which is dependent on θ. So I guess I do need a function of sorts?