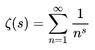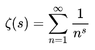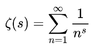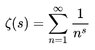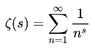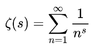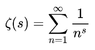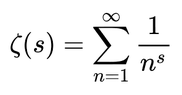Computing the Riemann Zeta Function Using Fourier Series

[stevendaryl]

Euler’s amazing identity
The mathematician Leonard Euler developed some surprising mathematical formulas involving the number $\pi$. The most famous equation is $e^{i \pi} = -1$, which is one of the most important equations in modern mathematics, but unfortunately, it wasn’t invented by Euler.Something that is original with Euler is this amazing identity:
Equation 1: $1 + 1/4 + 1/9 + 1/16 + … = \pi^2/6$
This is one instance of an important function called the Riemann Zeta function, $zeta(s)$, which in the case where $s > 1$ is defined by:
Equation 2: $\zeta(s) = \sum_{j=1}^\infty \dfrac{1}{j^s}$
So Euler’s identity can be written as:
Equation 3: $\zeta(2) = \frac{\pi^2}{6}$
This post is an attempt to show how you can derive that result, and related...

Continue reading...

 

[SSequence]

Just below the heading "Equation-7". Also same identity below the heading "Equation-9" and before "Sum-1".
$F(x)= \sum_{j=-\infty}^{\infty} e^{ijx}=\sum_{j=-\infty}^{-1} e^{ijx}+1+\sum_{j=0}^{\infty} e^{ijx}$

Shouldn't it be(?):
$F(x)= \sum_{j=-\infty}^{\infty} e^{ijx}=\sum_{j=-\infty}^{-1} e^{ijx}+1+\sum_{j=1}^{\infty} e^{ijx}$

 

[Svein]

Did you check out my Insight on this (Explore the Fascinating Sums of Odd Powers of 1/n Source https://www.physicsforums.com/insights/explore-the-fascinating-sums-of-odd-powers-of-1-n/ )? You will also find references to two earlier Insights, one of which shows how to calculate the Zeta function for all even values of s.

 

[stevendaryl]

Did you check out my Insight on this (Explore the Fascinating Sums of Odd Powers of 1/n Source https://www.physicsforums.com/insights/explore-the-fascinating-sums-of-odd-powers-of-1-n/ )? You will also find references to two earlier Insights, one of which shows how to calculate the Zeta function for all even values of s.

No, I had not read those. Thanks!

 

[Paul Colby]

Did you check out my Insight on this

I've checked chrome and safari and your link is broken in both. There appears to be garbage prior to the working URL. Is this the correct one?

Explore the Fascinating Sums of Odd Powers of 1/n Source https://www.physicsforums.com/insights/explore-the-fascinating-sums-of-odd-powers-of-1-n/

 

[Svein]

I've checked chrome and safari and your link is broken in both. There appears to be garbage prior to the working URL. Is this the correct one?

Yes. I have extended the results in that insight and I will update it Really Soon Now (as Jerry Pournelle used to say).