Computing the Thomas Precession: Help from PFers Needed!

[Coelum]

TL;DR Summary

While computing the transformation matrix associated to Thomas precession - as described by Goldstein (7.3) - I cannot reproduce a step in the derivation.

Dear PFer's,
I am reproducing the steps to derive the expression for the Thomas precession, as described in Goldstein/Poole/Safko "Classical Mechanics". Hereafter an excerpt from the book describing the step I am currently working on.

I have been able to compute the matrix L'' (eqn. 7.18). However, computing its approximation as described above (eqn 7.19 and γ' = 1), I get a different result:

.
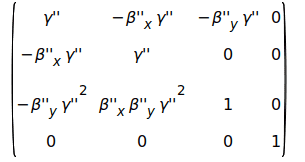As you can see, I get γ^2 rather than γ in the third row. I cannot find my mistake and I cannot see how γ can approximate γ^2. Any hint?
Thanks a lot in advance,

Francesco

 

[Coelum]

Just an idea: to first order in β, γ^2 ≈ γ since γ is quadratic in β. Sort of dirty trick, but formally correct?