Computing Thomas Precession: Part 2 | Francesco

[Coelum]

TL;DR Summary

While computing the transformation matrix associated to Thomas precession - as described by Goldstein (7.3) - I cannot reproduce a step in the derivation. This is a step later than the one described in my previous post "Computing the Thomas precession".

Dear PFer's,
I am reproducing the steps to derive the expression for the Thomas precession, as described in Goldstein/Poole/Safko "Classical Mechanics". Hereafter an excerpt from the book describing the step I am currently working on.

Based on the text, the transformation S_3 -> S_1 should be the composition of a boost on the x" axis

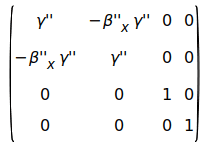
and a boost on the y" axis

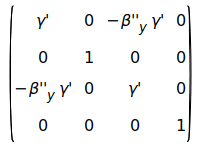
which, when composed assuming γ'=1, yield

.
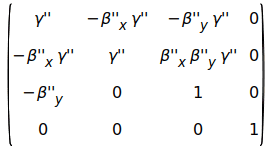The differences with (7.20) are:

1. the '-' sign in elements [1,2], [2,2], [2,1], [3,1]
2. the '0' in position [3,2]
3. the element in position [2,3], which can be approximated as (dropping the " for readability):
   β_xβ_yγ = γ(β_y/β_x)β_x² ≈ γ(β_y/β_x)β² = γ(β_y/β_x)(1-1/γ²) = (γ-1/γ)β_y/β_x. Close, but not identical.

Can anybody help me understand?

Thanks,

Francesco

 

[vanhees71]

The Thomas precession is hard to calculate. Here's my attempt (Sect. 1.8):

https://itp.uni-frankfurt.de/~hees/pf-faq/srt.pdf

 

[Coelum]

The Thomas precession is hard to calculate. Here's my attempt (Sect. 1.8):

https://itp.uni-frankfurt.de/~hees/pf-faq/srt.pdf

Hi vanhees71,
thanks for your answer! I am not familiar enough with Lie algebra to follow your exposition. But I understand I will need to learn the mathematical tools you are using if I want to dig deeper.

 

[vanhees71]

I think you don't need much more about Lie algebra than what's in this manuscript.

 

[vanhees71]

I think you don't need more about Lie algebra than what's in this manuscript to understand Fermi-Walker transport and thus the Thomas precession.

 

[dextercioby]

Not to sound like a wise guy, but I've always thought the treatment of J.D. Jackson (I have a translation of the 1975 edition) to be the best: lucid and straight to the point.

 

[Coelum]

Hi dextercioby, thanks for the pointer! In fact, the Thomas precession is discussed in section 11.8 of the second edition of Jackson's, though it requires reading the previous section on infinitesimal transformations.

As an update: I fixed all the issues except the '0' element in position [3,2]. That looks very strange: that element is certainly zero!

 

[Coelum]

Just an idea: to first order in β, γ"-1 ≈ 0. It can replace 0 in position [3,2]...