Concept of contour integration and integration along a square

[Amad27]

Hello,

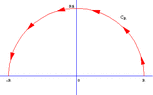
My question is, there is a concept of contour integration. Which is choosing a circular contour space sort of, and integrating along that.

How do you do contour integration?

Secondly, there is something going around called integrating along a square. I tried searching only, a lot, will anybody mind explaining this to me?

Also, what would it mean to integrate along an infinite square?

Thanks a lot =)

How is it possible to evaluate a series using complex methods?

 

[alyafey22]

You have to go through complex analysis first. I will give you a brief description.

Contour integration means that we are integrating a long a curve not along the real axis as we do with the usual integration. This requires Parametrization to be done in the first place.

There are common shapes that you integrate along to solve many integrals. For example , square , rectangle , circle , semi-circle , key-hole etc .. .

You can solve infinite series using contour integration but that requires an understanding many concepts like residues , Laurent expansion and Cauchy integral formula.

 

[Amad27]

You have to go through complex analysis first. I will give you a brief description.

Contour integration means that we are integrating a long a curve not along the real axis as we do with the usual integration. This requires Parametrization to be done in the first place.

There are common shapes that you integrate along to solve many integrals. For example , square , rectangle , circle , semi-circle , key-hole etc .. .

You can solve infinite series using contour integration but that requires an understanding many concepts like residues , Laurent expansion and Cauchy integral formula.

Okay.

But, how do you convert an integral from $-\infty$ to $+\infty$ to a closed circular contour?

How can the contour represent the whole interval from $-\infty$ to $\infty$

Also, what does it mean for an integral to vanish, and then it's residue sum $=0$?

Thanks ;D

 

[alyafey22]

Ok , I will try to explain the idea.

Suppose that you want to find a certain integral

$$\int^{\infty}_{-\infty} f(x) \,dx$$

The integral might be difficult to solve using real methods.

Assume that if we integrated the function $f$ along a closed curve we get a finite value.

For example if we integrate the function $f$ on the semi-circle below

View attachment 3525

Assume ,first, that the integral along the whole semi-circle is finite. The diameter of the circle (on the x-axis) is the integral we have to evaluate by taking $R \to \infty$. It remains to evaluate the integral along the curved part. Sometimes it is easy and evaluates to 0.

Integration Along the whole semi-circle = Integration along the diameter + Integration along the curved part = Integration along the diameter.

So we can write it as

$$\int^\infty_{-\infty} f(x) \,dx = \text{ Integration along the whole curve}$$

To evaluate the integration along the whole curve we have to use Residue theorem.

 

[alyafey22]

... Also, can you also help me through some complex analysis, and contour integration? I am quite interested, but I don't have means to learn it except MHB. Help will be appreciated! =)

You asked this question on the other thread. First , you need an introduction to complex numbers , if you haven't already studied it , you can take a look at this http://classes.soe.ucsc.edu/ams010/Spring11/complex_numbers_intro.pdf.

 

[Amad27]

You asked this question on the other thread. First , you need an introduction to complex numbers , if you haven't already studied it , you can take a look at this http://classes.soe.ucsc.edu/ams010/Spring11/complex_numbers_intro.pdf.

I have studied complex numbers, De Movire, Euler's Formula, etc.. before, but just not complex integration, which is by far the most interesting.

But why do you integrate along the whole curve?

The whole diameter is already from $-\infty \to \infty$ then why is the curved part needed??

 

[alyafey22]

I have studied complex numbers, De Movire, Euler's Formula, etc.. before, but just not complex integration, which is by far the most interesting.

Ok, let us then start with parameterization of curves. We know that the equation of circle is $x^2+y^2 = r^2$

How can I write it in terms of just one variable $t$.

But why do you integrate along the whole curve?

The whole diameter is already from $-\infty \to \infty$ then why is the curved part needed??

I will use symbols

$I_{\text{whole curve}} = I_{1}+I_{2} +\cdots +I_{n}$

It reads "The integration along the whole curve is equal to the integration of the sectors that form the whole curve".

Suppose we want to find $I_n$ and we can prove that $I_1 = I_2 = \cdots =I_{n-1} =0$ then

$I_{n} = I_{\text{whole curve}} $

We can find $I_{\text{whole curve}}$ using theory of residues.

 

[Amad27]

Ok, let us then start with parameterization of curves. We know that the equation of circle is $x^2+y^2 = r^2$

How can I write it in terms of just one variable $t$.
I will use symbols

$I_{\text{whole curve}} = I_{1}+I_{2} +\cdots +I_{n}$

It reads "The integration along the whole curve is equal to the integration of the sectors that form the whole curve".

Suppose we want to find $I_n$ and we can prove that $I_1 = I_2 = \cdots =I_{n-1} =0$ then

$I_{n} = I_{\text{whole curve}} $

We can find $I_{\text{whole curve}}$ using theory of residues.

There are infinitely many parametrizations for a single function.

$$x^2 + y^2 = r^2$$
$$y = \pm\sqrt{r^2 - x^2}$$

Let $x = \frac{t}{n}$ where $n \ge 1$

But from what I read you subtract the CURVE. So

$P = curve + diamater$

The integral on the entire real axis, negative infinity to infinity is

$I = P - Curve$

??

 

[alyafey22]

There are infinitely many parametrizations for a single function.

$$x^2 + y^2 = r^2$$
$$y = \pm\sqrt{r^2 - x^2}$$

Let $x = \frac{t}{n}$ where $n \ge 1$

I want the solution using complex numbers. You can use the fact that

$|z| = \sqrt{x^2+y^2}$

But from what I read you subtract the CURVE. So

$P = curve + diamater$

The integral on the entire real axis, negative infinity to infinity is

$I = P - Curve$

??

Yes , Now if we can prove that Curve=0 then it remains to evaluate $P$.

 

[Amad27]

I want the solution using complex numbers. You can use the fact that

$|z| = \sqrt{x^2+y^2}$

Now you have me stumped.

What this means is that:

$|z| = \sqrt{x^2+y^2} = r^2$

$a + bi = \cos(\theta) + i\sin(\theta)$

I am not quite sure.

How do you parametrize something with complex numbers?

 

[alyafey22]

Now you have me stumped.

What this means is that:

$|z| = \sqrt{x^2+y^2} = r^2$

$a + bi = \cos(\theta) + i\sin(\theta)$

I am not quite sure.

How do you parametrize something with complex numbers?

We know that we can write any complex number using the form

$$z = \sigma e^{i\theta}$$

Hence we have $|z|=\sigma$

So the definition of the circle is $x^2+y^2 = r^2$

$$|z| = \sqrt{x^2+y^2}=r $$

Hence we have

$$z = re^{i\theta} $$

So if $r=1$ the unit circle can be written as

$$z=e^{i\theta}$$

Now we want to parametrize the circle of radius 2 and centre (0,1). How can we do that ?

 

[Amad27]

We know that we can write any complex number using the form

$$z = \sigma e^{i\theta}$$

Hence we have $|z|=\sigma$

So the definition of the circle is $x^2+y^2 = r^2$

$$|z| = \sqrt{x^2+y^2}=r $$

Hence we have

$$z = re^{i\theta} $$

So if $r=1$ the unit circle can be written as

$$z=e^{i\theta}$$

Now we want to parametrize the circle of radius 2 and centre (0,1). How can we do that ?

I don't understand a few things.

How is $|z| = \sigma$?

If $z = \sigma e^{i\theta}$ then

$\sigma e^{i\theta} = \sigma\cos(\theta) + i\sigma \sin(\theta)$
$|\sigma e^{i\theta}| = |\sigma\cos(\theta) + i\sigma\sin(\theta)| = |\sigma (a) + \sigma (b)(i) = \sigma\cdot\sqrt{a^2 + b^2}$

So your assumption is that $a,b = 1$? But why?

 

[alyafey22]

I don't understand a few things.

How is $|z| = \sigma$?

If $z = \sigma e^{i\theta}$ then

$\sigma e^{i\theta} = \sigma\cos(\theta) + i\sigma \sin(\theta)$
$|\sigma e^{i\theta}| = |\sigma\cos(\theta) + i\sigma\sin(\theta)| = |\sigma (a) + \sigma (b)(i) = \sigma\cdot\sqrt{a^2 + b^2}$

So your assumption is that $a,b = 1$? But why?

No , use the equality

$$\sqrt{\sin^2+\cos^2 } = 1$$

 

[Amad27]

No , use the equality

$$\sqrt{\sin^2+\cos^2 } = 1$$

Actually, I think there's a simpler way.

$|z| = \sqrt{x^2 + y^2} = r$

$\sigma |z| = r\sigma$

Is that the result we are looking for?

 

[alyafey22]

Actually, I think there's a simpler way.

$|z| = \sqrt{x^2 + y^2} = r$

$\sigma |z| = r\sigma$

Is that the result we are looking for?

No, we want to find the parametrization of circle. We want to prove that

$$z = e^{it}$$

is a parametrization of the unit circle. By taking the absolute value

$|z| = 1$

hence that represents all points on the plain that are of the same distance =1 from the origin. This is actually the definition of circle.

I suggest you review complex numbers before continuing the discussion.

 

[Amad27]

No, we want to find the parametrization of circle. We want to prove that

$$z = e^{it}$$

is a parametrization of the unit circle. By taking the absolute value

$|z| = 1$

hence that represents all points on the plain that are of the same distance =1 from the origin. This is actually the definition of circle.

I suggest you review complex numbers before continuing the discussion.

I though you wanted it for a general radius?

So I am confused, what am I supposed to parametrize?

 

[alyafey22]

I am just providing an example to make it easier. The question is find the parametrization of the circle of radius $r$ and centre (0,0).

 

[Amad27]

I am just providing an example to make it easier. The question is find the parametrization of the circle of radius $r$ and centre (0,0).

I think we should do what we did for the other thread.

Can you perhaps show me step-by-step for radius $1$ ? I can then try radius $r$ by myself??

 

[alyafey22]

Any complex number can be written using

$$z = x+iy= \sigma e^{i\theta}$$

where $|z|= \sigma = \sqrt{x^2+y^2} $

Now, for the unit circle we know that $x^2+y^2 = 1$. This can be written as $ \sqrt{x^2+y^2} = 1$. So $\sigma = 1 $. Hence the unit circle can be written as

$$z = e^{i\theta} $$

 

[Amad27]

Any complex number can be written using

$$z = x+iy= \sigma e^{i\theta}$$

where $|z|= \sigma = \sqrt{x^2+y^2} $

Now, for the unit circle we know that $x^2+y^2 = 1$. This can be written as $ \sqrt{x^2+y^2} = 1$. So $\sigma = 1 $. Hence the unit circle can be written as

$$z = e^{i\theta} $$

I still have the same question.

How is $|z| = \sigma$?

Because it is the "hypotenuse" of the right triangle?

 

[alyafey22]

$$|z| = |\sigma||e^{i\theta}| = \sigma |\sin \theta +i\cos \theta | = \sigma\sqrt{\cos^2 \theta +\sin^2 \theta} = \sigma$$

 

[Amad27]

$$|z| = |\sigma||e^{i\theta}| = \sigma |\sin \theta +i\cos \theta | = \sigma\sqrt{\cos^2 \theta +\sin^2 \theta} = \sigma$$

So we have to deal with $x^2 + y^2 = r^2$

In the form $z= ge^{it}$

This is actually just euler's formula isn't it?

$z = g(e^{it}) = g(\cos(t) + i\sin(t))$

Geometrically, how is the absolute value $\sqrt{\sin^2(t) + \cos^2(t)}$?Plotting a point assuming $\sin(t), \cos(t) \ne 0$

We get the "y" point as $i\sin(t)$
We get the "x" point as $\cos(t)$

The pythagorean theorem says,

$(i\sin(t))^2 + (\cos(t))^2 = |z|^2$

$\sqrt{-\sin^2(t) + \cos^2(t)} = |z| \ne 1$

 

[alyafey22]

We get the "y" point as $i\sin(t)$
We get the "x" point as $\cos(t)$

No , the $y$ point is $\sin(t)$. $y$ is the imaginary part of the complex number $z = x+iy$.

Please read this article.

 

[Amad27]

No , the $y$ point is $\sin(t)$. $y$ is the imaginary part of the complex number $z = x+iy$.

Please read this article.

I understand.

QUESTION:
Is this because distance is just a positive number, so in imaginary terms, "distance," is equal to $i\sin(t)/i$ because distance is a REAL-SCALAR number?

Thanks

 

[alyafey22]

I understand.

QUESTION:
Is this because distance is just a positive number, so in imaginary terms, "distance," is equal to $i\sin(t)/i$ because distance is a REAL-SCALAR number?

Thanks

Yeah , you can think about it like that. Actually any point $(x,y)$ can be written as $x+iy$. So we know that the distance between the origin and $(x,y)$ is $\sqrt{x^2+y^2}$. The same is done when we have $cos t+i\sin t = (\cos t,\sin t)$.

PS: I hope you had time to read the whole article. It is very nice and will help you in the future.

 

[Amad27]

Yeah , you can think about it like that. Actually any point $(x,y)$ can be written as $x+iy$. So we know that the distance between the origin and $(x,y)$ is $\sqrt{x^2+y^2}$. The same is done when we have $cos t+i\sin t = (\cos t,\sin t)$.

PS: I hope you had time to read the whole article. It is very nice and will help you in the future.

Let's say we have$r(z^{it}) = r(\cos(t) + i\sin(t))$

$|r(z^{it})| = r$

$|z^{it}| = 1$

I am severely confused, how should I do this? Can you show me?

 

[alyafey22]

Let's say we have$r(z^{it}) = r(\cos(t) + i\sin(t))$

$|r(z^{it})| = r$

$|z^{it}| = 1$

I am severely confused, how should I do this? Can you show me?

I suppose you mean $e^{it}$ not $z^{it}$ ?

 

[Amad27]

I suppose you mean $e^{it}$ not $z^{it}$ ?

Yes