- #1
CheeseSandwich
- 4
- 0
I am learning about the polar coordinate system, and I have a few conceptual questions.
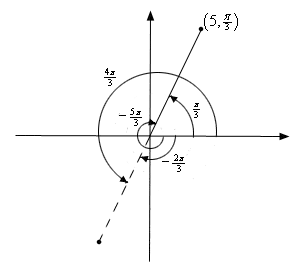
I understand that in Cartesian coordinates there is exactly one set of coordinates for any given point. However, in polar coordinates there is an infinite number of coordinates for a given point. I see how they are derived visually in the diagram below, and I see how the coordinates are derived by the expressions below.
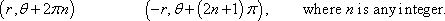
Here are my questions:
Thanks!
CheeseSandwich
I understand that in Cartesian coordinates there is exactly one set of coordinates for any given point. However, in polar coordinates there is an infinite number of coordinates for a given point. I see how they are derived visually in the diagram below, and I see how the coordinates are derived by the expressions below.
Here are my questions:
- I see how infinite coordinates can be derived, but why can there be infinite coordinates for one point?
- How can a point in the first quadrant be equivalent to a point in the third quadrant?
- Why can't we represent the point (5, π/3) in the second or fourth quadrants? Why does n have to be an integer and not a rational number?
Thanks!
CheeseSandwich