Conceptual question involving tension and angles

[pandatime]

Homework Statement

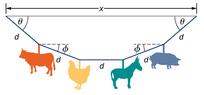
Hanging from the ceiling over a baby bed, well out of baby’s reach, is a string with plastic shapes, as shown here. The string is taut (there is no slack), as shown by the straight segments. Each plastic shape has the same mass m, and they are equally spaced by a distance d, as shown. The angles labeled θ describe the angle formed by the end of the string and the ceiling at each end. The center length of sting is horizontal. The remaining two segments each form an angle with the horizontal, labeled ϕ. Let T1 be the tension in the leftmost section of the string, T2 be the tension in the section adjacent to it, and T3 be the tension in the horizontal segment. (a) Find an equation for the tension in each section of the string in terms of the variables m, g, and θ. (b) Find the angle ϕ in terms of the angle θ. (c) If θ=5.10°, what is the value of ϕ? (d) Find the distance x between the endpoints in terms of d and θ.

Relevant Equations

F_g = mg
equations to split vector into component form using cos(theta) and sin(theta)
a*b = |a||b|cos(theta) (to find angles of vectors)

I have actually already partly solved a), as I do get the concept behind how to find tension through making sure that the net force in the x and y direction are zero.

Here are my answers for a)
T1 = T5 = 2mg/sin(theta)

T2 = T4 = mg/sin(phi)

T3 = mg*cot(phi)

The reason I am asking this question here is because I cannot figure out how to write phi in terms of theta, which is what b) asks me to do.

I've tried to rearrange
T1 = 2mg/sin(theta)
T1sin(theta)=2mg
(T1sin(theta))/2 = mg

and then plugging it into my T2/T4 equation
so, T4=(T1sin(theta))/2)/sin(phi)

but then I don't know how to get rid of T1, in the T4 equation, as the question explicitly tells me to write my answers in terms of m, g, and theta.

I looked at the answer key to try to nudge me in the right direction and for some reason the answer is phi = arctan(1/2tan(theta)).

I'm thinking that maybe the T3 equation would play a hand in the answer, because it's my only equation that has tan(theta) in it somewhere.

I don't think I see any angle rules that relate phi to theta either, so I couldn't solve it that way.

That being said, any guidance would be appreciated in finding out how to write phi in terms of theta

 

[kuruman]

Hi @pandatime and welcome to PF.

It would help if you showed how you got the answer for T1. If I were you, I would draw a free body diagram of the knot where the cow is attached to the string and set the sums of vertical and horizontal forces equal to zero. Is that you did? You should get two equations involving T1, T2, and trig functions of θ and ϕ. Repeat for the second knot and see what you get.

Should you need additional help, please post all your work, not just the bottom lines that you got. It would be very helpful if you wrote your equations in LaTeX. Click on the link "LaTeX Guide" at the lower left corner above the "Suggested for:" box.

 

[pandatime]

Hi there! thank you for your advice

The way that I got my answer for $T_1$, and basically all the other tensions was through free body diagrams of each, I think explaining it would be enough to suffice because I'm not anywhere where I can draw right now.

I did free body-diagrams of each animal individually, for example, for the cow, I drew that there was an $F_g$ and $T_1$ and $T_2$ force on it, and I split the $T_1$ and $T_2$ forces into component forces and redrew the FBDs with the component forces instead. I then found out that in the y-direction, $F_g + T_4 sin\phi = T_5 sin\theta$. (This simplifies to $T_5 = \frac{2mg}{sin\theta}$ BECAUSE of the FBD that I made for the horse, where we find through the same process that $T_4 sin\phi = mg$ since those are the only forces in the y-direction acting on the horse.

I believe this explanation is enough? Let me know if I was not clear enough though!

As I said, I think my answers for a) are right, so there shouldn't be any problems with that part, but really struggling on writing $\phi$ in terms of $\theta$...

Oh.. I'm having trouble, I thought I could just type in the latex like it does in stack exchange? It's not showing up

 

[pandatime]

Am I doing something wrong regarding the latex? is that not the right way to type it?

 

[Lnewqban]

Am I doing something wrong regarding the latex? is that not the right way to type it?

Welcome!
Use double symbol ($$ or ##) before and after it.

 

[kuruman]

Am I doing something wrong regarding the latex? is that not the right way to type it?

You need to bracket your expression between double dollar signs ($$) for this site. You can also use double pound signs ## for inline rendering.

 

[pandatime]

Welcome!
Use double symbol ($$ or ##) before and after it.

You need to bracket your expression between double dollar signs ($$) for this site. You can also use double pound signs ## for inline rendering.

Am I not using "$" before and after math symbols? I thought I did in my reply? Or is it not visible? Sorry to bother :( Like why is$ \theta ## not working?

 

[pandatime]

Am I not using "$" before and after math symbols? I thought I did in my reply? Or is it not visible? Sorry to bother :( Like why is$ \theta ## not working?

uhh... idk what happened, I did not change anything in the reply that didn't render the latex, and it all just rendered like JUST NOW. I have no idea why it just chose to render

well this is good! since now you guys can probably read my reply and explanation behind my equations!

 

[Lnewqban]

If you superpose the two FBD's that you have created, you could clearly see how both angles are geometrically related.
Both triangles of forces and components share the same base.

 

[pandatime]

ahhh sorry to ask, but english isn't my first language, what is superpose?

 

[Lnewqban]

ahhh sorry to ask, but english isn't my first language, what is superpose?

To place one right or rectangled triangle of forces on or above the other, so that their legs or catheti (base and height) coincide.

 

[haruspex]

idk what happened, I did not change anything in the reply that didn't render the

While you are typing in, it will not show the rendered form. To see that without hitting Post, tap the magnifying glass icon at top right of the data entry area. If it still does not render, do a page refresh and tap it twice more.
To resume editing, tap it again.

 

[haruspex]

how to write phi in terms of theta

You have only considered vertical forces.

 

[jbriggs444]

Am I not using "$" before and after math symbols? I thought I did in my reply? Or is it not visible? Sorry to bother :( Like why is$ \theta ## not working?

The reason that the above post renders poorly is the first, stand-alone "##". When you want one of those not to render, the easiest trick is to switch colors on the second # symbol. Force it to black using the palette icon.

With BBcode rendering turned off (use the [ ] icon for that) it looks like: "#[COLOR=rgb(0, 0, 0)]#[/COLOR]". As you can see, the two # symbols are no longer back to back, which is why the trick works.